Je passai le lendemain à lire tout ce que je pouvais concernant les treillis. Il en existe de multiple formes – treillis complets, distributifs, complémentés… Tout un bestiaire. J’étais en train de parcourir une liste de références quand mon œil fut attiré par un titre prometteur. Laissant tomber tout le reste, je me précipitai sur l’article en question que je dévorai ; puis, excité mais fatigué, j’allai faire une sieste, car je ne voulais pas attendre la nuit pour faire part à Galois de ma découverte du jour.

De ce fait je fis un rêve en horaire décalé et retrouvai dans son bureau un Evariste Galois en bras de chemise, sirotant une tasse de café en feuilletant son journal.

– Tiens ? Vous êtes là ! Je ne vous attendais pas à cette heure-ci.

– J’espère ne pas vous déranger, mais en parcourant divers articles concernant les treillis, j’ai trouvé quelque chose qui pourrait grandement nous aider. Il existe, de fait, un champ des mathématiques appelé analyse formelle des concepts, qui s’appuie justement sur la notion de treillis !

– Ma foi, voilà qui paraît en effet très intéressant. Je ne crois pas avoir entendu parler de ce domaine, me ferez-vous la gentillesse de m’en toucher un mot?

– Avec grand plaisir ! D’autant que ces mathématiciens ont peut-être déjà résolu mon problème !

– Nous verrons cela. Allez-y mon cher, je suis tout ouïe.

– L’idée est d’extraire une série d’objets appelés « concepts » d’un ensemble de données. Ces « concepts » se trouvent être organisés en treillis.

– A quoi ressemblent ces données dont vous parlez?

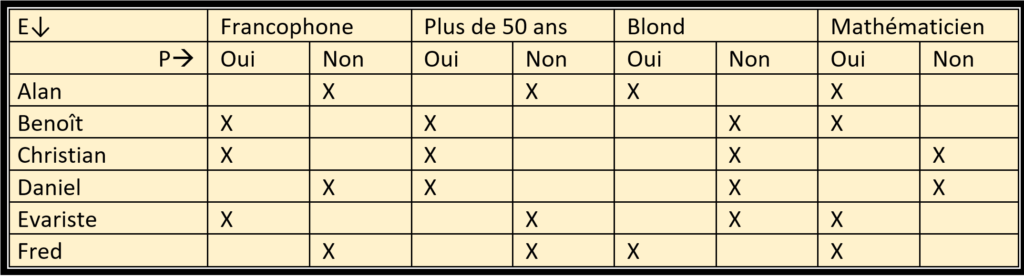
– On considère un ensemble E d’objets ou individus quelconques, et un ensemble I d’attributs que chaque objet peut, ou non, présenter. Prenons l’exemple d’un ensemble de personnes. Chacune de ces personnes peut ou non parler Français, être mathématicien, être blond, avoir moins de 50 ans, etc. Nous pouvons représenter la relation entre les objets et les attributs par un tableau à double entrée, comme ceci :

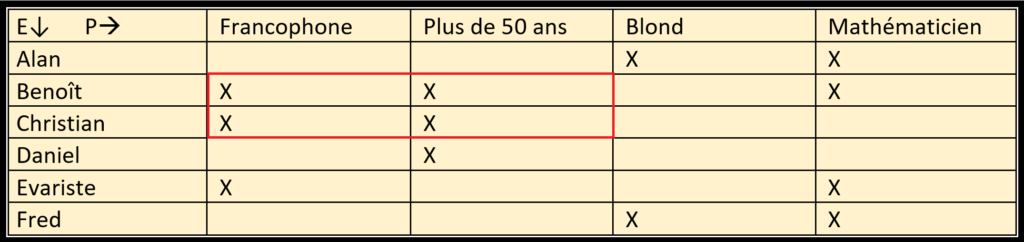
Puis nous recherchons des rectangles maximaux dans ce tableau. Un rectangle est défini par un ensemble d’entités choisies parmi celles de E et un ensemble d’attributs choisis parmi ceux de I, de façon que chacun des objets choisis présente tous les attributs choisis : si on réordonne les lignes et les colonnes de façon à rendre contigus les objets et les attributs choisis, on obtient un rectangle rempli de croix. Dans mon exemple, Benoît et Christian forment un rectangle avec les attributs « Parle Français » et « Plus de 50 ans », ce que l’on peut voir en réorganisant le tableau :

– A chaque fois que l’on change l’ordre des lignes et des colonnes, on voit apparaître de nouveaux rectangles ; il peut donc y en avoir beaucoup.

– Oui. Mais parmi tous les rectangles qui existent, on élimine ensuite tous ceux qui sont contenus dans un autre. Par exemple, le rectangle horizontal défini par Benoît et les deux attributs « Parle Français » et « Plus de 50 ans » est contenu dans celui dont nous venons de parler ; c’est aussi le cas pour le rectangle vertical défini par Benoît, Christian et l’attribut « Parle Français ».  En éliminant tous les rectangles de ce type, il ne reste que ceux qui ne sont contenus dans aucun autre, qu’on appelle rectangles maximaux. Dans un rectangle maximal, on ne peut pas ajouter une personne sans perdre au moins une propriété, et on ne peut pas ajouter une propriété sans perdre au moins une personne. Dans notre exemple, le rectangle que nous avons identifié est maximal ; on trouve aussi entre autres le rectangle défini par Alan, Benoît, Evariste et Fred avec le seul attribut « Mathématicien », mais aussi celui défini par Benoît qui est l’unique mathématicien francophone de plus de cinquante ans. Ce sont ces rectangles maximaux qui sont appelés concepts dans la théorie.

– Je vois. C’est astucieux. Je comprends que l’on puisse considérer ces rectangles comme des concepts, car ils représentent à la fois un ensemble d’objets individuels et l’ensemble des attributs communs à ces objets. Cela me fait penser à un ouvrage dont m’a beaucoup parlé mon ami Blaise, malheureusement publié l’année de son décès, et qu’il n’a donc pu lire que post mortem – ce qui est mieux que rien, j’imagine.

– Oui, la Logique de Port Royal. Ce livre a proposé les notions que nous appelons maintenant extension et intention d’un concept. L’extension, c’est l’ensemble d’individus concrets qui ressortissent d’un concept donné ; l’intention, c’est l’ensemble des propriétés (ou, en logique moderne, des prédicats) qui définissent la signification du concept et doivent être vérifiés par chaque individu. L’extension du concept de triangle, c’est l’ensemble de tous les triangles qui existent, panneau « céder le passage » inclus ; l’intention du concept de triangle, c’est la propriété d’avoir trois côtés. En ces termes, on peut donc dire qu’un concept est défini par son extension et son intention, de manière symétrique.

– Vous m’avez dit que ces concepts sont organisés en treillis. Que dit la théorie à ce sujet ?

– D’abord il faut se rappeler que deux concepts, vus comme des rectangles maximaux, ne sont jamais inclus l’un dans l’autre. Cela implique que si l’extension de l’un est incluse dans l’extension de l’autre, alors son intention ne l’est pas, et vice-versa. En fait, l’extension d’un concept s est incluse dans celle d’un concept g si et seulement si l’intention de g est incluse dans celle de s : l’ensemble des objets de s est plus restreint que celui de g parce que s impose plus de propriétés à respecter que g. On peut donc définir un ordre de généralisation entre concepts en disant que s ≼ g si l’extension de s est contenue dans celle de g ou, ce qui est équivalent, si l’intention de g est contenue dans celle de s. On peut montrer que, muni ce cet ordre, l’ensemble des concepts forme un treillis. Et il y a une surprise….

– Laquelle?

– Eh bien, en Français, ce treillis de concepts est appelé Treillis de Galois en votre honneur !

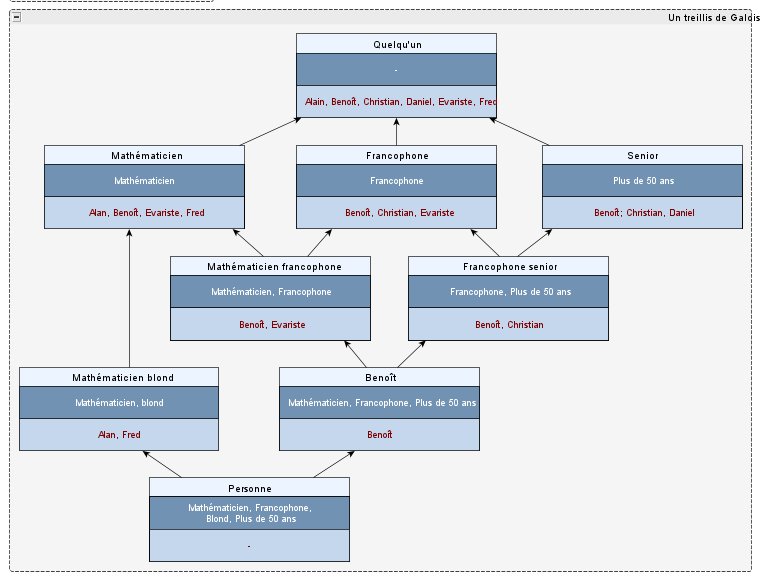
– Je suis très touché! Tiens, essayons de dessiner le treillis correspondant à votre exemple. Sauf erreur de ma part, il me paraît correspondre à ceci :

Vous le voyez, j’ai mentionné sous son nom l’intention et l’extension de chaque concept. Vous remarquerez que le concept minimal, [Personne], a une extension vide et une intention qui contient toutes les propriétés ; à l’inverse le concept maximal, [Quelqu’un], a une intention vide et une extension qui contient toutes les personnes.

– Il est curieux qu’il n’y ait pas de concept pour Alan ni pour Christian, par exemple ? Ne les avez-vous pas oubliés ?

– Non. Notez d’une part que Alan et Fred ont exactement les mêmes propriétés, et ne sont donc pas distinguables par ces dernières. Tout concept dont l’extension contient Alan concerne aussi Fred et vice-versa. En fait, du point de vue conceptuel Alan et Fred sont une même personne puisque rien ne les distingue.

– Ils n’ont pourtant pas le même nom !

– Certes, mais nous n’avons pas choisi d’associer une propriété au nom d’une personne. Nous aurions pu le faire, en ajoutant une propriété pour chaque nom, par exemple « s’appelle Alan », « s’appelle Benoît », etc. Dans ce cas nous aurions obtenu une propriété et un concept par personne, car chaque personne aurait été seule à s’appeler par son nom. Mais tel n’est pas le cas dans votre exemple. D’un point de vue philosophique, il me paraît par ailleurs parfaitement sain de décréter que deux objets ayant les mêmes propriétés sont identiques ; car tout ce que nous pouvons connaître d’un objet, ce sont ses propriétés. Pour ce que nous en savons, ici Alan et Fred sont la même personne, affublée d’un surnom. Non, cet aspect du formalisme ne me pose aucun problème.

 – Je vois. Mais Christian, alors ? sa combinaison de propriétés est unique. C’est le seul qui soit francophone de plus de 50 ans et rien d’autre !

– « Et rien d’autre » : voilà ce qui vous piège. La définition que vous m’avez proposée pour les concepts ne prend pas en compte l’absence d’une propriété pour un individu donné ; seulement sa présence. Nous savons que chaque propriété de Christian est également une propriété de Benoît, mais c’est tout. Les deux sont des francophones de plus de 50 ans. Benoît, en plus, est mathématicien. Mais Christian ne se distingue pas de Benoît, car il n’a aucune propriété additionnelle. L’absence d’une propriété n’est pas une propriété. Vous noterez d’ailleurs que ce formalisme n’identifie pas non plus un concept des moins de 50 ans, ou des non-francophones, ou des non-mathématiciens. Pour la même raison il ne peut donc pas identifier Christian comme francophone de plus de 50 ans non mathématicien.

– Je trouve cela regrettable, décevant. Je peux tout de même penser à Christian en tant qu’individu unique ; il devrait vraiment y avoir un concept pour lui. Quant au pauvre Daniel, il n’apparaît que comme un senior anonyme ! Tout ça pour ça ? J’ai bien peur de vous avoir dérangé pour rien…

– Bien au contraire. Si vous êtes déçu la faute n’en revient pas au formalisme, mais bien au choix de votre exemple. Vous avez proposé des propriétés un peu au hasard, à la va-vite. Si vous aviez spécifié un propriété « 50 ans ou moins » à la place de « Plus de 50 ans », par exemple, vous auriez obtenu des concepts très différents. Si vous aviez proposé une propriété « nul en maths », c’est Benoît qui n’existerait plus en tant que concept. Je vous propose donc d’être plus systématique et de considérer chaque attribut « Parle Français », « Blond », etc. non pas comme une propriété mais comme une question à laquelle on répond oui ou non pour chaque personne. C’est cette réponse que nous considérerons comme une propriété attachée à la personne. Regardez ce que devient votre tableau :

Vous voyez que nous avons à présent huit propriétés, et que chaque personne possède exactement quatre d’entre elles. Le nouveau treillis de concepts (que je ne dessinerai pas car il est bien plus complexe) possède maintenant des concepts comme « non mathématicien », « non francophone », ou « ni mathématicien ni francophone ». Daniel et Christian y ont chacun leur propre concept. Alan, en revanche, y reste confondu avec Fred, car ils ont toujours les mêmes propriétés ; mais nous pourrions, comme nous l’avons dit, noter si chaque personne s’appelle ou non Alan, ce qui nous permettrait de les distinguer.

– C’est superbe ! Cela suggère que notre subjectivité manipule un treillis de Galois construit de cette manière, à partir de propriétés binaires qui décrivent notre état en assignant la valeur « oui » ou « non » à différentes questions binaires !

– Hmmm… Votre enthousiasme fait plaisir à voir, mais je ne serais pas aussi catégorique. Quelque chose me dit que nous sommes loin d’avoir fait le tour de la question. Mais je sens que vous allez vous réveiller, et j’ai pour ma part un rendez-vous à honorer. Nous reverrons-nous demain pour en parler ?

– Avec plaisir !

Puis, avisant la fleur accrochée au revers de sa veste soigneusement posée sur le dos de la chaise, et remarquant l’effluve particulièrement raffiné de son après-rasage, il me vint à l’esprit que son rendez-vous pourrait bien être de nature à lui faire oublier l’infâme coquette ; aussi lui dis-je dans un grand sourire :

– Et surtout bonne chance, Evariste ! Amusez-vous bien !

à suivre…