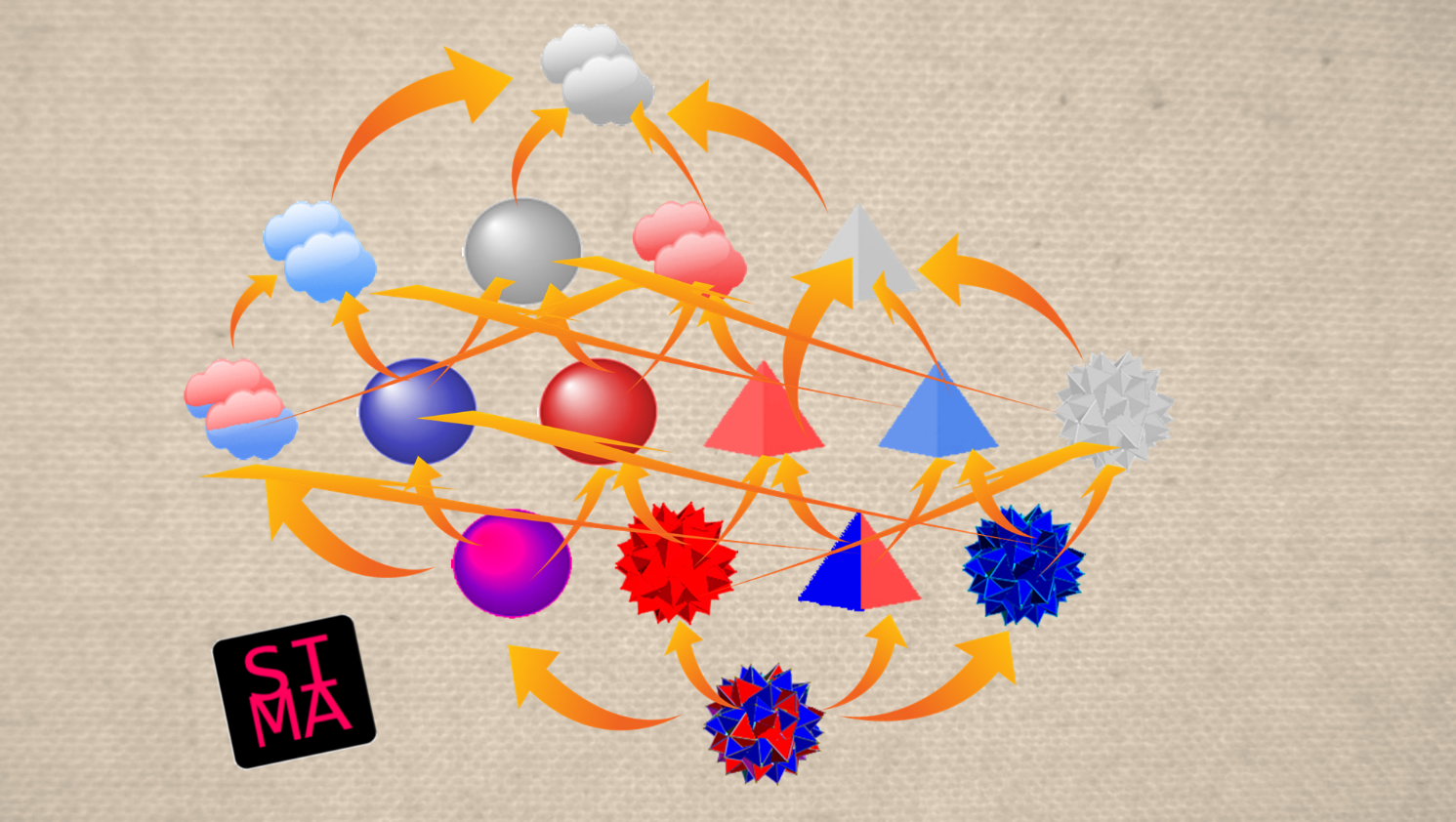
Nous nous retrouvâmes donc la nuit suivante dans le bureau de Galois, toujours sans l’œil de taureau qui semblait encore digérer les événements du mois précédent. Corty nous projeta l’œuvre de Sima sur le tableau, et Galois l’étudia en silence pendant un long moment.
– « Le songe d’Everett » … J’aime bien le titre. Bien que ce travail soit fort éloigné des canons de mon époque, je lui reconnais une force étrange, un peu hypnotique. Le regard file d’une forme à l’autre en suivant les flèches, sans pouvoir s’échapper du labyrinthe. Merci de me l’avoir montré, mes amis.
Corty intervint :
– Nous pensons, Maître, que ce dessin mériterait également une étude plus analytique, en rapport avec nos discussions. Sima prétend que les concepts manquants dont vous parliez y figurent. En particulier, le symbole le plus à gauche serait le concept de forme, et celui à l’opposé le concept de couleur. C’est tout ce que nous avons pu en tirer.
– Voyons, dit Galois… Tout d’abord, nous devons nous rappeler que ce treillis n’est évidemment pas un treillis de concepts subjectifs ; il est bien trop symétrique, et surtout les éléments en sont définis individuellement, pas par leurs rapports entre eux. En revanche, si je comprends l’intention de l’artiste, ce treillis est censé représenter l’ensemble des concepts que l’on pourrait extraire d’un monde (sursimplifié) de formes colorées. Si c’est bien le cas, cela veut dire que toute conscience vivant dans un tel monde formerait un treillis de concepts subjectifs obtenus en sélectionnant certains de ces concepts et en en rejetant d’autres, de façon à éliminer symétries et redondances.
– Il faudra revenir là-dessus, répliquai-je. Nous aurons besoin de mieux comprendre comment et pourquoi des concepts subjectifs pourraient émerger d’un treillis de concepts « objectifs » aussi symétrique.
– Certes, dit Galois, mais pour le moment il convient, comme l’a proposé Corty, d’analyser plus précisément ce treillis.
– On peut utiliser le premier dessin de Sima, celui qu’il a abandonné, comme base. Le voici pour mémoire:
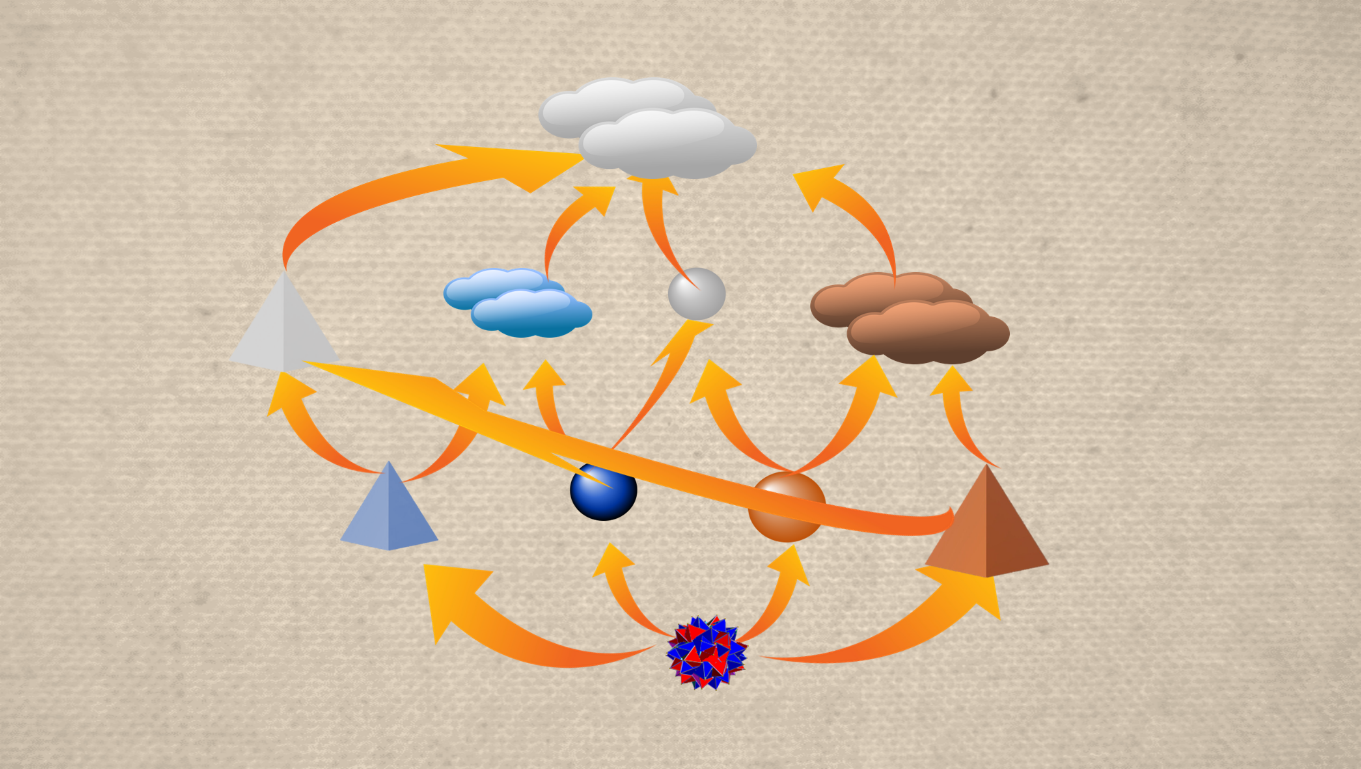
Par exemple, le nuage rouge y représente l’ensemble des objets rouges des deux formes possibles, et la grenade en bas le concept d’une forme impossible qui serait à la fois un cercle et un triangle. Or nous retrouvons des nuages et des grenades dans l’œuvre définitive.
– De même, ajoutai-je, la pyramide incolore représente l’ensemble des triangles des deux couleurs, et la grenade bicolore expose également une couleur impossible, qui serait à la fois rouge et bleue. Or on retrouve des symboles incolores et d’autres bicolores dans le Songe d’Everett.
– Parfait, dit Galois. Nous devrions donc pouvoir utiliser ce code pour donner un sens à tous les symboles du dessin final. Par exemple, la grenade rouge représenterait une forme impossible mais de couleur rouge. La pyramide bicolore, elle, représenterait un triangle de couleur impossible.
– Le nuage bicolore à gauche du Songe d’Everett représente alors n’importe quelle forme mais avec une couleur impossible, et la grenade incolore à droite représente une forme impossible mais de n’importe quelle couleur. Or Sima nous dit que la première est le concept de forme, et la seconde le concept de couleur.
– Il y a une certaine logique à cela, répondit Galois. Je crois que Sima nous montre la différence entre le concept de forme ou de couleur – en tant qu’attribut d’un objet – et le concept d’objet qui possède une forme et une couleur. De même, il ou elle nous montre la différence entre le concept, disons, de triangle – en tant que forme pure – et la collection des objets colorés de forme triangulaire. En fait, son idée est de réifier les attributs et propriétés, c’est-à-dire de considérer un attribut ou une propriété d’un objet comme un concept en soi. La grenade rouge, par exemple, c’est la couleur rouge : elle n’existe qu’en tant que couleur, et ne se définit pas en termes de forme ; c’est pourquoi elle présente la « forme impossible ». Ce concept se différencie du nuage rouge qui, lui, représente l’ensemble des objets rouges. De même, la sphère bicolore représente le concept pur de cercle en tant que propriété de forme d’un objet, alors que la sphère incolore représente l’ensemble des objets circulaires rouge ou bleu.
– Dans ce cas, dit Corty, l’interprétation que donne Sima du nuage bicolore est correcte. Ce nuage représente l’ensemble des deux formes pures – triangle et cercle – sans référence à une notion de couleur (d’où l’emploi de la couleur impossible). Il s’agit bien d’un concept de forme au sens le plus pur du terme. De même, la grenade incolore est l’ensemble des deux couleurs pures, sans référence à une notion de forme. Je crois que nous en savons assez pour donner des noms aux concepts du Songe d’Everett. Je vous propose ceci :
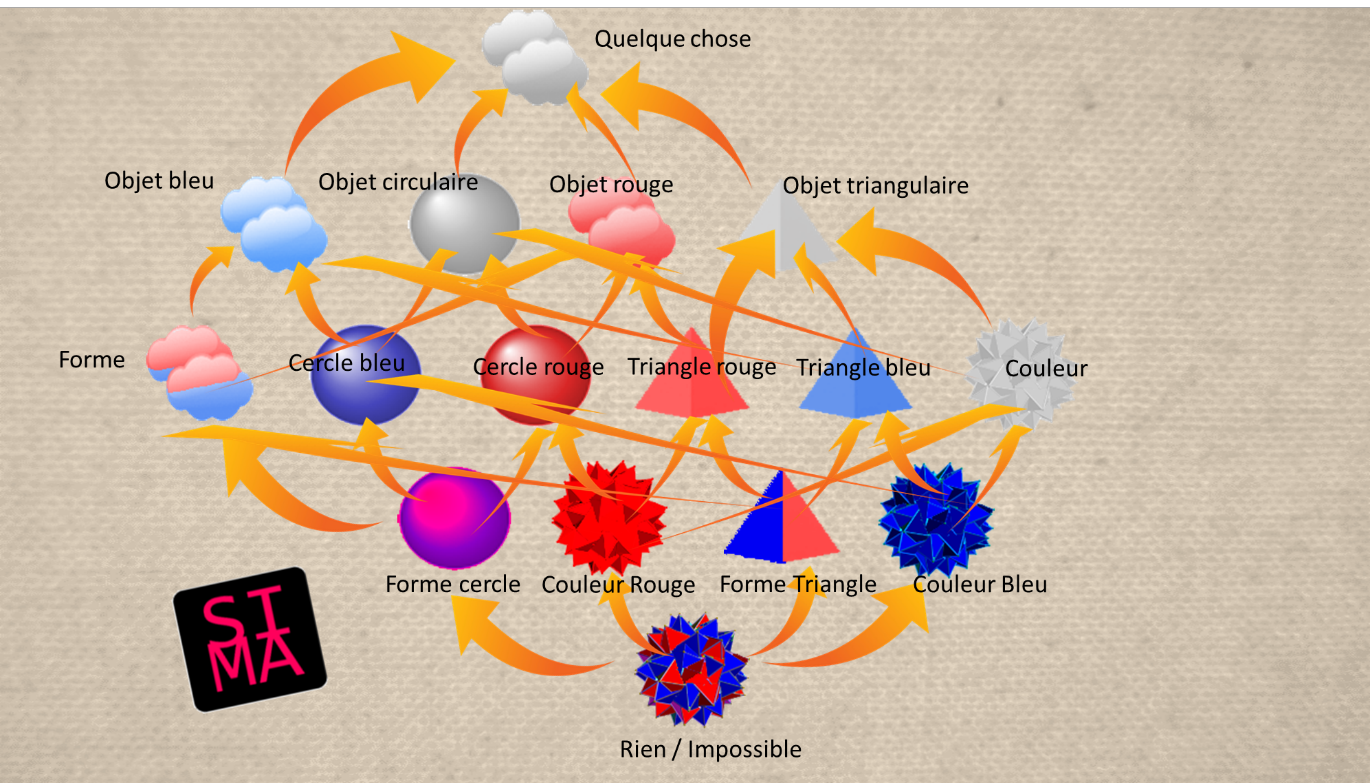
– Cela me paraît plus clair, dis-je. Reste à comprendre les flèches. Comment interpréter celle entre « forme triangle » et « triangle rouge », par exemple ? En quoi représente-t-elle une généralisation ? Un triangle rouge est un triangle, pas l’inverse.
– Oui, mais dans la phrase que vous venez de prononcer, « un triangle » désigne l’ensemble des objets triangulaires, c’est-à-dire la pyramide incolore. Or il y a bien une flèche entre les concepts « triangle rouge » et « objet triangulaire ». Dans le cas qui vous préoccupe, la forme triangle doit être vue comme une propriété, en l’occurrence une propriété du triangle rouge. Nous pouvons donc dire « la forme triangle est une des propriétés du triangle rouge (l’autre étant la couleur rouge) ». Il me paraît donc juste de considérer que le concept « forme triangle » spécialise le concept « triangle rouge » si l’on considère l’intention de ce dernier, c’est-à-dire l’ensemble de ses propriétés. De même, il est vrai que tout objet a une forme, donc le concept Forme est un attribut de tout objet, par exemple des triangles rouges. C’est( encore une autre forme de spécialisation. Bien sûr, cela change nous un peu de tous nos exemples précédents, où nous ne manipulions que des objets et des ensembles d’objets, mais Abel nous a prévenu contre le risque de surinterprétation de ces exemples.
– Je comprends, intervint Corty. Je remarque d’ailleurs quelque chose d’intéressant. Si je vous demande « quelle est la couleur du triangle rouge », vous me répondrez « la couleur rouge ». Eh bien, j’observe que dans ce treillis la conjonction de l’objet « triangle rouge » et de l’attribut « couleur » est justement la propriété « couleur rouge ». Autrement dit, je peux obtenir la valeur d’un attribut d’un objet, comme sa forme ou sa couleur, en calculant la conjonction de l’objet et de l’attribut, et j’obtiens la propriété correspondante.
– Mais oui ! dis-je tout excité. C’est assez fascinant, en fait. En programmation, très souvent, nous distinguons des objets (disons, un objet appelé triangleRouge), leurs attributs (des noms dont chacun désigne une de leur propriété, comme forme ou couleur), et les valeurs possibles pour ces propriétés (comme triangle ou rouge). Pour obtenir la couleur d’un objet, j’écrirais typiquement une expression comme triangleRouge.couleur, qui me donnerait la valeur de l’attribut couleur pour l’objet triangleRouge. Notre treillis nous donne la même chose, tout en unifiant les objets, leurs attributs et les valeurs de ces derniers dans une seule représentation. C’est très élégant. D’autres formalismes offrent cette unification formelle, mais je ne m’attendais pas à la trouver dans un treillis…
– … Et encore moins dans une œuvre d’art, je suppose, dit Galois. Mais je viens de penser à autre chose encore. Je crois avoir compris d’où l’inconscient de Sima a tiré ce dessin. Savez-vous ce qu’est un produit de treillis ?
– Non, Maître, déclara Corty. Je n’ai rien lu sur ce terme. Yannick non plus, par définition.
– Eh bien, supposez que vous ayez deux treillis A et B. Vous pouvez construire l’ensemble « produit » de A et B, dont les éléments sont tous les couples formés d’un élément de A et d’un élément de B. Maintenant, choisissons deux tels couples. Nous dirons que leur conjonction est le couple qui contient d’une part la conjonction des deux éléments de A qu’ils contiennent, et d’autre part la conjonction des deux éléments de B. Nous définissons la disjonction de deux couples de la même manière. Nous obtenons ainsi un nouveau treillis, qui est le treillis produit de A et B.
– D’accord, je vois à peu près. Poursuivez, Maître.
– Eh bien, considérez maintenant des objets décrits uniquement par leur forme, triangulaire ou circulaire. Avec un exemple de chaque, nous obtenons un treillis de Galois que je schématise ici (vous me pardonnerez de ne pas avoir le talent de Sima):
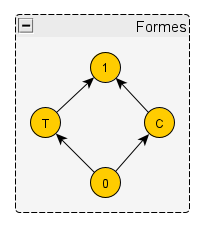
Pour des raisons que vous comprendrez très vite, j’ai adopté une convention assez usuelle qui donne le nom 0 à l’élément minimal d’un treillis et 1 à son élément maximal. Ici, 0 désigne le concept, dont l’extension est vide, d’objets qui sont à la fois triangulaires et circulaires ; T et C désignent les concepts d’objets triangulaires et circulaires ; 1 désigne le concept de tous les objets (son intention étant vide).
Je dessine un treillis de Galois analogue pour des objets décrits uniquement par leurs couleurs :
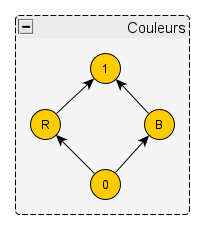
Et je dessine maintenant le produit de ces deux treillis. Chaque élément est nommé en concaténant le nom d’un élément du premier avec le nom d’un élément du deuxième. Voici ce que nous obtenons :
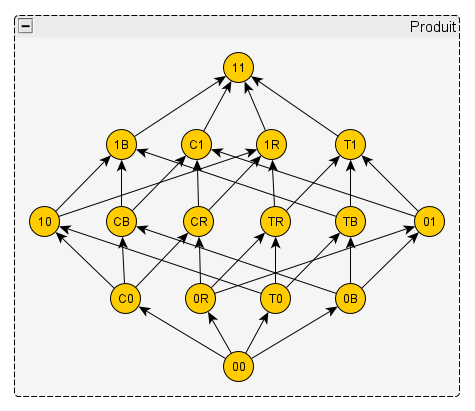
– Ça alors ! Mais c’est exactement le même treillis que le Songe d’Everett !
– Parfaitement. Sima n’a peut-être pas la bosse des maths, mais son inconscient me paraît assez doué. Ce que nous avons ici, c’est un treillis particulier qu’on appelle également une algèbre de Boole, comme d’ailleurs les deux petits treillis dont il est le produit. Il se trouve que George, auquel ce nom est dû, a longtemps été mon voisin à l’hôtel Aleph. Vous avez peut-être entendu parler de la logique Booléenne utilisée dans vos ordinateurs : eh bien, c’est à lui qu’on doit tout ça. Excellent joueur de bridge, par ailleurs. Un peu snob à mon goût peut-être, surtout compte tenu de ses origines somme toute modestes ; mais enfin, c’est un Anglais, il faut faire avec, n’est-ce pas. Bref, voici éclairci le mystère du Songe d’Everett.
– Passionnant, m’enthousiasmai-je.
– J’ai malheureusement un rendez-vous qui m’oblige à en rester là, conclut Galois, dont le sourire de plaisir anticipé démentait ouvertement les propos. Je vous propose donc de résumer nos découvertes d’aujourd’hui. Je crois que nous disposons grâce à Sima d’une nouvelle manière de fabriquer des concepts objectifs qui pourront servir de matière première à nos concepts subjectifs, si je puis dire. L’idée en est que si plusieurs attributs indépendants sont associés à un même objet, au lieu de calculer un treillis de Galois unique qui les prenne tous en compte en même temps, nos perceptions s’appuient sur le treillis obtenu en calculant le produit de différents petits treillis, chacun associé à un de ces attributs. Nous considérons la forme d’un côté, la couleur de l’autre, et nous construisons des concepts plus riches de cette manière, comme la notion d’une forme ou de la couleur rouge. Cela, effectivement, comble le manque que je ressentais depuis longtemps.
– Quelle belle avancée ! Nous sommes sortis du marasme, me semble-t-il.
– Espérons-le, dit une petite voix bougonne. Je ne veux plus jamais revivre une catastrophe pareille.
C’est le caillou. Pour le meilleur ou pour le pire, il est revenu.








0 commentaires