La nuit même, je me retrouvai dans le bureau de Galois, éclairé par un joli soleil de printemps. Je ne l’avais jamais vu aussi net et pimpant : on y sentait une touche féminine, et puis visiblement Corty avait sorti le grand jeu question rendu. Galois lui-même rayonnait, élégant comme tout dans sa veste d’intérieur sur l’épaule de laquelle je distinguai un fin et long cheveu blond, un sourire béat aux lèvres. Il m’accueillit chaleureusement.

– Si j’en crois les rumeurs, on dirait que vous avez du nouveau ? Je suis impatient d’entendre en détail ce que vous avez découvert !

– Bien volontiers Maître ! Je suis venu avec Corty, mon cortex visuel, que vous connaissez. Il est tout autant à l’origine de nos derniers progrès que moi.

– Bonjour, Maître, intervint Corty en cursives maniérées sur le tableau noir. C’est un honneur et un plaisir de discuter avec vous.

– Bienvenue, bienvenue à vous. C’est un beau travail que vous avez fait tous les trois !

Tous les trois ? Qu’est-ce que… C’est alors que je découvris l’Œil de Taureau, que la logique du rêve avait confortablement déposé en plein soleil sur le bureau de Galois. Le petit salopard jubilait. De fait, je l’entendis ronronner de plaisir sous le compliment. Force m’était cependant de reconnaître qu’il avait effectivement sa part dans nos avancées récentes.

– Bien, dit Galois, je vous propose d’abord de résumer rapidement ce que vous avez découvert depuis notre dernière discussion. Si je comprends bien, vous avez joué avec de petits treillis de Galois (pardon d’utiliser ce terme présomptueux) fabriqués à partir de certaines combinaisons de propriétés visuelles, les couleurs d’un côté, les niveaux de gris de l’autre. Vous avez déterminé que ces treillis représentent correctement votre perception subjective et consciente de ces éléments visuels, à condition de subir certaines transformations, qui ont en commun l’effet de limiter l’ensemble des concepts subjectifs à ceux qui vous sont réellement utiles, et que votre cerveau semble effectuer par des mécanismes de bas niveau issus de millions d’année d’évolution. Vous avez plus précisément identifié deux mécanismes de transformation de treillis. L’un consiste à éliminer du treillis des concepts inutiles voire nuisibles (il jeta un coup d’œil vers le caillou) ; l’autre consiste à fusionner certains concepts redondants. Vous avez enfin établi, ce qui me paraît essentiel, que seuls des concepts symétriques (dans un sens qu’il nous faudra mieux définir) peuvent être fusionnés. Est-ce que ce résumé vous paraît exhaustif ?

Nous murmurâmes en chœur notre assentiment. Ce jeune homme avait le chic pour extraire la substance d’une idée en quelques phrases.

– Dans ce cas, je vous propose maintenant de couper le problème en deux. Je suggère d’oublier temporairement tout ce que nous savons sur les treillis de Galois, et de nous concentrer sur la structure de votre treillis de concepts subjectifs, que vos trouvailles devraient nous permettre de préciser.

– Pourquoi cette approche, Maître ? demanda Corty.

– Pour plusieurs raisons. Tout d’abord, la notion de treillis de Galois –treillis fondé sur les rectangles d’une relation binaire entre une collection d’objets ou situations et leurs propriétés – nous offre une piste très intéressante pour comprendre comment nous formons des concepts à partir de nos perceptions physiques de base, mais rien ne garantit ni n’impose que cela soit le seul mécanisme permettant de créer des concepts subjectifs dans un système conscient en général. Je pense intuitivement qu’il peut y en avoir d’autres. En tout état de cause, un concept subjectif, tel que nous l’avons défini, ne spécifie pas s’il représente un rectangle reliant une extension et une intention, ou bien tout autre chose ; l’esprit conscient ne manipule ni objets ni propriétés, mais seulement des concepts. Souvenez-vous que quand nous avons commencé à aborder le problème, nous sommes convenus qu’il n’y avait aucun autre objet du discours à considérer que le concept et ses relations avec d’autres concepts ; je pense important de maintenir ce principe tant que nous ne sommes pas forcés de l’abandonner.

–Vous favorisez l’économie conceptuelle, si je puis me permettre ce jeu de mot, risquai-je.

– Exactement, et je cherche à conserver la plus grande généralité possible. Si nous pouvons déterminer des propriétés du treillis de concepts subjectifs qui soient indépendantes de la manière dont ces concepts sont formés, nous pourrons appliquer ces résultats dans d’autres contextes.

– Me voilà convaincu, écrivit Corty.

– Il y a une autre raison, continua Galois. Il se trouve qu’être « de Galois » n’impose aucune contrainte structurelle à un treillis ; on peut facilement prouver que tout treillis, quel qu’il soit, peut être considéré comme le treillis de Galois d’une certaine relation. De ce point de vue, « treillis de Galois » et « treillis quelconque », c’est la même chose. Nous pouvons donc laisser le côté « treillis de Galois » de côté pour le moment ; en revanche nous y reviendrons certainement plus tard, car je pense que nous n’avons pas du tout fait le tour de la manière dont les concepts se forment.

– Parfait, intervint l’œil de Taureau. Vous me plaisez, vous. Vous savez trancher. Pas comme tous ces chnops qui tergiversent sans arrêt.

– Euh… merci. Donc, concentrons-nous sur les propriétés structurelles d’un treillis de concepts subjectifs que nous pouvons dériver de vos expériences récentes. La première que je voudrais traiter, car elle me paraît essentielle, est celle-ci : un treillis de concepts subjectifs ne contient jamais de symétries. En effet, deux concepts symétriques sont redondants et sont subjectivement (voire physiquement) fusionnés.

– Je comprends ce que vous entendez par « fusion physique », intervint Corty, car c’est exactement ce qu’effectue mon architecture neuronale. Mais qu’entendez-vous par « fusion subjective » ?

– Ce que je veux dire par là, c’est que même si vous, Corty, vous ne vous chargiez pas d’intégrer physiquement les signaux provenant des bâtonnets situés dans une même zone, la conscience de Yannick ne pourrait de toute façon jamais avoir accès à des concepts tels que « bâtonnet 1 actif » ou « bâtonnet 2 actif ». La raison en est que (comme vous l’avez-vous-même bien décrit) ces concepts subjectifs joueraient exactement le même rôle vis-à-vis de tous les autres. Or, nous avons de fait décrété qu’un concept subjectif n’est défini que par ses relations avec tous les autres.  Par définition, si ces relations sont les mêmes pour deux concepts subjectifs, alors ces concepts n’en font qu’un. Attention, il s’agit là d’une hypothèse très forte, très signifiante. Mais elle était présente dès le début de nos discussions, et vos expériences m’ont convaincu de sa validité.

– Donc, dit le caillou, le cerveau des chnops ne fait qu’économiser de l’énergie en leur évitant de manipuler des concepts qu’ils ne pourraient de toute façon pas distinguer ?

– Exactement. Mathématiquement, notre définition du concept subjectif n’impose pas qu’un mécanisme physique calcule réellement cette fusion ; mais il est certainement avantageux pour un être vivant…

– … ou pas…

– … d’éviter des manipulations d’information redondantes que la subjectivité confondra de toute façon.

– Je crois comprendre ce que vous dites, dis-je, mais ça me parait fort de café. Je ne pourrais pas distinguer consciemment ces concepts de niveau de gris, même si mon cerveau ne faisait pas le travail de les fusionner physiquement, parce qu’ils auraient exactement les mêmes relations avec tous les autres concepts que je connais. Ce ne seraient même pas des synonymes, parce que des synonymes ont au moins des noms différents, donc une relation différente avec les concepts sonores.

– Exactement. Si je vous dis qu’il y a un concept de rocher et un autre concept de rocher, mais que je suis incapable de vous expliquer la différence entre les deux, qu’en conclurez-vous ?

– Que vous êtes cinglé comme un chnops et qu’il n’y a pas d’autre rocher que le rocher, conclut l’œil de taureau. Ça tombe sous le sens. Continuons.

– Je suis bien d’accord, émit Corty, mais il faudrait définir cette histoire de symétrie. Je la trouve un peu floue. C’est d’ailleurs une des raisons pour laquelle nous voulions vous rencontrer, Maître.

– Très bien, dit Galois. Allons-y pour un peu de maths. Vous savez ce qu’est une fonction, n’est-ce pas ? C’est une association par laquelle chaque élément d’un certain ensemble dit « de départ » est associé à un élément d’un ensemble dit « d’arrivée », appelé son image. Yannick a écrit là-dessus au début de cette histoire (mon cher ami René en est d’ailleurs encore tout meurtri). Prenons un treillis donné T comme ensemble de départ et aussi comme ensemble d’arrivée : nous considérons une fonction qui à chaque élément de ce treillis en associe un autre (ou lui-même). Nous noterons y = f(x) si x est un élément du treillis, y est l’image de x, et f est la fonction.

– OK, dit le caillou. Même un chnops peut comprendre ça.

– Maintenant, nous imposons une condition sur f, qui est de respecter la structure du treillis. Plus précisément, nous demandons que l’image de la conjonction de deux concepts soit la conjonction des images de ces deux concepts, ce qui s’écrit mathématiquement :

∀x,y ∈ T², f(x ⋏ y) = f(x) ⋏ f(y)

Et de même pour la disjonction :

∀x,y ∈ T², f(x ⋎ y) = f(x) ⋎ f(y)

Si la fonction f respecte ces règles, nous l’appelons un endomorphisme du treillis T.

– « Etat ou action de forme interne ». J’adore le Grec, s’excita l’œil de taureau. Saviez-vous que j’ai passé une après-midi dans la bouche de Démosthène, il y a quelques temps de ça ?

Galois ne se laissa pas démonter par l’interruption.

– Vous serez alors ravi d’apprendre cet autre mot : automorphisme. Il désigne un endomorphisme tel que deux concepts différents ont toujours des images différentes, et où tout concept est l’image d’un autre concept (unique). Un automorphisme peut être inversé : à partir de l’image, on retrouve l’antécédent qui l’a produite. On parle aussi d’endomorphisme bijectif.

– Bijectif, du latin. Pouah. Une langue de barbares, si vous voulez mon avis.

– Soyez rassuré, on ne le veut pas, continua Galois. Voilà, nous avons le vocabulaire nécessaire pour définir cette histoire de symétrie.

– Allez-y, Maître, écrivit Corty. Nous sommes toute ouïe, si je peux dire. Et toi, le caillou, tais-toi un peu. Yannick ne sait peut-être pas où est planqué le marteau, mais moi si.

– Vous remarquerez d’abord que dans n’importe quel treillis, il existe toujours un automorphisme dit trivial : c’est la fonction qui, à chaque concept, associe ce même concept. On appelle cette fonction l’identité. Elle ne change rien à rien. Bien évidemment, elle satisfait les propriétés demandées.

– Bien évidemment ! dit l’œil de taureau. Même le dernier des chnops… euh, continuez, Maître.

– Quand il existe d’autres automorphismes que l’identité, le treillis contient des concepts « symétriques » : deux éléments différents du treillis sont symétriques si l’un est l’image de l’autre par un automorphisme.

– Je vois. Puis-je me permettre de proposer un exemple ou deux, Maître ? intervint Corty.

– Mais je vous en prie. Vos capacités graphiques sont impressionnantes, et les miennes un rappel constant à l’humilité.

Corty dessina ceci :

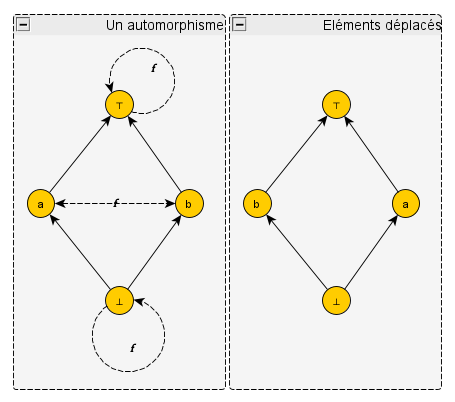
– Dans cet exemple, nous avons un treillis très simple avec un automorphisme f qui associe chaque élément à son image comme représenté par les lignes pointillées. Les deux éléments minimal (⊥) et maximal (⊤) sont chacun leur propre image. L’image de a est b, et l’image de b est a. A côté, j’ai représenté le dessin qu’on obtient quand on bouge chaque élément à la place de son image. J’ai remarqué que dans le cas d’un automorphisme, les deux dessins sont identiques et peuvent se superposer. Ici, par exemple, si l’on échange a et b on obtient le même dessin.

– Parfait ! Dit Galois. Dans ce dessin, a et b sont effectivement symétriques ; chacun est même l’image de l’autre.

– J’ai aussi pensé à un autre exemple plus compliqué. Ici aussi, quand on déplace chaque élément vers l’emplacement de son image, on obtient le même dessin :

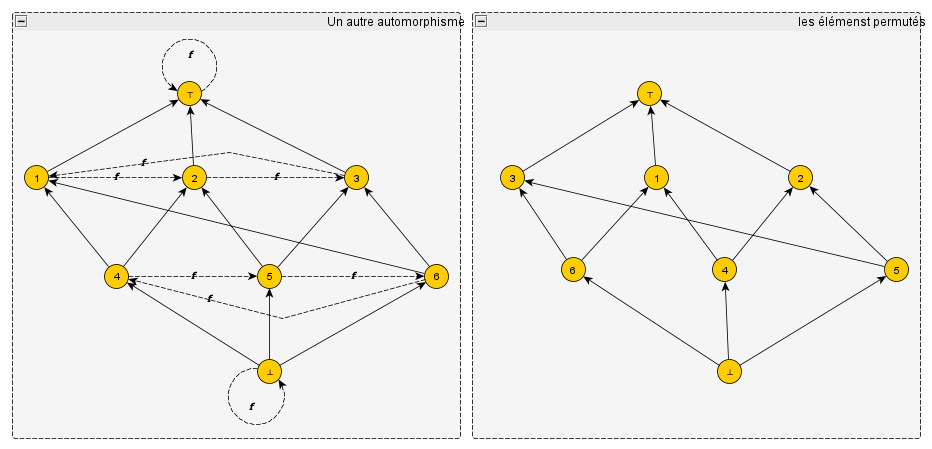
– Intéressant, dit Galois. Dans cet exemple, les éléments 1, 2 et 3 opèrent une permutation circulaire, tout comme les éléments 4, 5 et 6. De ce fait, les éléments 1 et 2 sont symétriques, de même que 2 et 3. Mais du coup, 1 et 3 sont également symétriques, car il suffit d’appliquer l’automorphisme f deux fois de suite pour passer de l’un à l’autre, or la composition de deux automorphismes est aussi un automorphisme. Nous nous retrouvons donc avec un groupe de trois éléments tous symétriques les uns des autres : 1,2 et 3.  De même les éléments 4,5 et 6 sont symétriques les uns des autres.

–  D’accord, dis-je. Cela me paraît clair. Que se passe-t-il alors dans le cas qui nous intéresse ?

– Eh bien, notre hypothèse est qu’un treillis de concepts subjectifs ne contient aucune symétrie ; en d’autres termes, il ne possède pas d’autre automorphisme que l’identité. En effet, si deux ou plusieurs concepts étaient symétriques les uns des autres, ils se retrouveraient fusionnés en un seul.

– Corty, pourrais-tu dessiner un exemple d’un tel treillis sans symétrie ? J’avoue que j’ai du mal à l’imaginer.

– Tu m’étonnes ! En voici un :

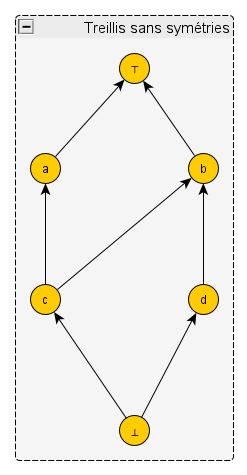– Dans cet exemple, on ne peut pas permuter les éléments d’une manière qui reproduise le même dessin. Par exemple, si l’on échangeait a et b, ou c et d ou les deux, cela créerait une flèche orientée du bas à droite vers le haut à gauche, qui n’existe pas dans le dessin d’origine.

– C’est un bon indice, dit Galois, même si ça ne constitue pas une preuve. Si nous voulions prouver formellement que ce treillis ne possède aucun automorphisme autre que l’identité, il nous faudrait considérer toutes les permutations possibles des 6 éléments et montrer qu’à chaque fois au moins une des contraintes imposée aux endomorphismes est violée. Bien sûr ce n’est pas très difficile dans ce cas, et on peut gagner du temps en se disant que les éléments maximal et minimal sont forcément leur propre image ; cependant, c’est un problème difficile dans le cas général, en ce sens que le nombre d’étapes nécessaires pour le résoudre augmente exponentiellement avec la taille du treillis.

– Cela veut dire que notre cerveau doit faire ce travail monstrueux, pour identifier tous les concepts symétriques et les fusionner ?

– Non, dit Galois, et c’est ce qui est assez magique selon moi. Certains concepts fondamentalement symétriques, nous l’avons vu, sont physiquement fusionnés par les couches basses de Corty ou d’autres parties de votre cerveau. L’évolution a simplement sélectionné cette solution plus simple et plus économique. Il est possible en revanche que d’autres symétries persistent physiquement dans la représentation que votre cerveau donne à ses concepts, même si cela me paraît très improbable vu la complexité et l’asymétrie du monde réel. Mais même si c’était le cas, subjectivement, vous ne verriez aucune différence entre deux concepts symétriques, car vous n’auriez rien pour les distinguer. Identifier et fusionner tous les concepts symétriques, ce qui représenterait un travail monstrueux,  n’est donc pas nécessaire au fonctionnement de votre conscience ; en d’autres termes, votre treillis de concepts subjectifs ne contient aucune symétrie même si le système physique sous-jacent qui encode vos concepts en contient peut-être. Votre treillis de concepts subjectifs n’a en fait pas besoin d’être explicitement calculé pour exister ; pour vous, il est pourtant la seule chose qui existe.

– Je trouve ça bien mystérieux, dis-je.

– Moi aussi, intervint Corty

– Moi de même, dit le caillou.

– Et moi tout autant, dit Galois, mais il me semble que cette conclusion est rendue inévitable par les hypothèses que nous avons adoptées jusqu’à présent. Bien entendu, nous avons toujours la possibilité de revenir en arrière si nécessaire.

Un chœur de protestations s’éleva.

– Pas maintenant, en tout cas !

– Je suis d’accord avec vous, dit Galois ; nous sommes en train d’explorer une piste prometteuse à l’aide d’un formalisme assez élégant, autant aller aussi loin que possible.