Rechercher si la conscience peut émerger dans une machine est un voyage au long cours à bord d’un improbable esquif philosophico-mathématique. Quel qu’en soit le point d’arrivée, il offre l’occasion de découvertes et de rencontres parfois déconcertantes mais riches d’enseignements…Je me retrouvai la nuit suivante dans le bureau de Galois. J’y trouvai ce dernier en train de discuter avec Corty par tableau noir interposé. Enfin, discuter, c’est vite dit :  le tableau était couvert de mots d’esprit d’Oscar Wilde, d’une grille de morpion, et même (me sembla-t-il) de quelques vers licencieux à-demi effacés.  Du caillou, point de trace.

Galois se précipita vers moi quand il me vit.

– Mon ami, Corty et moi avons répondu à votre appel et tuions le temps en vous attendant. Auriez-vous par hasard des nouvelles un peu réjouissantes à nous apporter ?

– Ce serait bien, écrivit Corty. Nous étions sur le point de commencer une partie de bataille navale. Pour te dire à quel point on s’amuse, ici.

Je me fis une joie de leur résumer mon échange avec Abel et mes réflexions concomitantes.

Le visage de Galois s’éclaira :

– Bravo! Et merci ! Vous féliciterez de ma part votre étrange ami d’être intervenu avec tant de talent pour nous remettre sur le droit chemin. Il me faut bien l’admettre : depuis quelques temps, je manque un peu de concentration, sinon je n’aurais jamais laissé passer une erreur pareille. Cependant, il y a des moments où, n’est-ce pas…

– Je comprends parfaitement, Maître. Ô combien. Et, si je puis me permettre de le dire, je me réjouis pour vous.

– Moi de même, renchérit Corty. Heureusement qu’il n’y a pas que les maths dans la vie !

Nous restâmes silencieux quelques minutes, chacun pensant à qui, dans sa vie, importait somme toute bien plus que les maths. Cette étrange communion prit fin quand un rire de gorge d’une pureté de cristal jaillit dans ma tête. Mon cortex auditif était heureux. L’entendre était certes réjouissant, mais me fit me sentir un peu voyeur, si je puis me permettre d’employer ce terme. Il fallait revenir au présent :

– Il me semble que nous disposons de nouvelles bases de nature, je l’espère, à nous permettre de résoudre nos problèmes en suspens. Qu’en dites-vous, Maître ?

– Oui, je le pense. Je vous félicite, vraiment bravo.

Je me sentis sur un petit nuage.

­– Cependant…

Je sentis mon petit nuage s’effilocher.

– Cependant, je me permettrai de suggérer une formulation légèrement plus formelle et concise de votre proposition, que voici : Un treillis de concepts subjectifs est un treillis fini dans lequel le seul endomorphisme tel que les images de deux éléments non comparables soient non comparables est l’identité.

– …. Et ? balbutiai-je.

– Je crois bien que c’est tout, dit Galois. Sauf, bien entendu, si quelque chose m’échappe.

– J’en serais bien surpris, intervint Corty. Votre résumé, maître, est d’une clarté cristalline.

Je retombai brutalement au sol.

J’avais déjà connu le ridicule de débattre (du côté perdant) avec un caillou obstiné, l’humiliation de me sentir intellectuellement inférieur à mon propre cortex visuel, la migraine due aux altérations intempestives de mon champ visuel par ce dernier, le désespoir de voir mes efforts apparemment réduits à néant par le susdit caillou – mais je n’avais pas encore touché le fond, pas avant de me sentir jaloux d’une conscience onirique géniale issue de mon inconscient (ou du monde platonicien des Idées, allez savoir). La jalousie mesquine est un sentiment que j’exècre, lectrice, et je ne suis pas fier de l’avoir éprouvé à cet instant. Mais le fait est que Galois venait d’exprimer très précisément, en une phrase et quelques minutes, ce que j’avais mis plusieurs pénibles semaines et sept pages à définir laborieusement. Il y a de quoi être un peu vexé.

Fort heureusement, ce vilain sentiment laissa immédiatement la place à un élan d’admiration sans borne. Car, de fait, l’énoncé de Galois offrait une synthèse rigoureuse et d’une grande élégance à mes considérations quelque peu dispersées, le tout en n’utilisant que des concepts mathématiques déjà bien établis, ce qui est toujours souhaitable.

Reprenons pas à pas ce que Galois venait de dire : Un treillis de concepts subjectifs est un treillis fini dans lequel le seul endomorphisme tel que les images de deux éléments non comparables soient non comparables est l’identité.

Vous vous en souvenez peut-être, un endomorphisme de treillis est une fonction qui associe à chaque élément du treillis un élément identique ou différent du même treillis, appelé son image ; de plus l’image de la conjonction de deux éléments est la conjonction de leurs images, et de même pour leur disjonction. Tout treillis présente un ou plusieurs endomorphismes : par exemple l’identité, qui associe chaque élément à lui-même ; ou encore les endomorphismes constants, qui associent tous les éléments à l’un d’entre eux choisi une fois pour toute. L’image du treillis par un endomorphisme, qui contient les images de tous ses éléments, est également un treillis – le treillis de départ lui-même ou un sous-ensemble.

Galois considère les endomorphismes qui obéissent à une condition supplémentaire : si deux éléments ne sont pas comparables (aucun des deux n’est « plus petit » que l’autre), alors leurs images ne le sont pas non plus. Certains endomorphismes comme l’identité ont cette propriété, d’autres ne l’ont pas. Galois exige que le seul endomorphisme ayant cette propriété soit l’identité. Pourquoi cela ?

Rappelez-vous que j’ai proposé de définir un treillis de concepts subjectifs T en assignant un nom à chaque élément, et en faisant la liste de toutes les lignes (a, b, c, d) dans lesquelles a et b sont les noms de deux éléments non comparables du treillis, c le nom de leur conjonction et d le nom de leur disjonction. Mon but était de reconstruire le treillis à partir de ces égalités, en prouvant que c’est le plus petit treillis qui les respecte, que les noms de de chaque ligne désignent quatre éléments différents, et qu’une seule affectation d’un nom à un concept est possible.

S’il existe un endomorphisme de T qui respecte la condition proposée par Galois, je peux affecter un nom (ou plusieurs) à chaque élément du treillis image de T. Pour cela, j’affecte simplement le nom d’un élément à son image – ce qui peut me conduire à affecter plusieurs noms à un même élément, car plusieurs éléments peuvent avoir la même image.

Chaque ligne de noms (a,b,c,d) de la définition de T désigne dans ce nouveau treillis les images de a,b, a ⋏ b et a ⋎ b. Comme a et b ne sont pas comparables, leurs images ne le sont pas non plus ; par ailleurs l’image de a ⋏ b est bien la conjonction des images de a et b, et l’image de a ⋎ b est leur disjonction. Tous les éléments identifiés par chaque ligne dans le treillis image sont ainsi différents et respectent les égalités qui définissent T.

De ce fait, s’il existe plusieurs endomorphismes qui satisfont la condition proposée par Galois (et pas seulement l’identité), alors il existe plusieurs treillis possibles, ou plusieurs affectations de noms aux éléments d’un même treillis, qui satisfont la définition de T. Les éléments de T ne sont pas uniquement déterminés par cette définition, et T n’est donc pas un treillis de concepts subjectifs. A l’inverse, s’il existe un treillis plus simple que T ou une autre affectation des noms aux éléments qui satisfait la définition de T, alors on peut prouver qu’il existe un endomorphisme de T qui satisfait la condition de Galois.

On remarque par ailleurs qu’un treillis symétrique présente un automorphisme (un endomorphisme qui permute les éléments, chacun étant l’image d’exactement un autre élément ou de lui-même) différent de l’identité. Or un automorphisme respecte la condition de Galois ; un treillis symétrique n’est donc pas un treillis de concepts subjectifs. De même, si deux concepts sont redondants comme Chien et Animal, la fonction qui associe Chien et Animal à Animal et tout autre élément à lui-même est un endomorphisme qui respecte cette même condition ; un tel treillis n’est donc pas non plus un treillis de concepts subjectifs. Nous retombons bien sur nos pattes. Cet homme est génial.

Certes. Seulement voilà : Galois trouve peut-être tout ça évident, Corty peut penser que c’est limpide, mais pour moi tout ça n’a rien de simple. Pour prouver ce qui précède, il faut par exemple utiliser un résultat d’algèbre universelle – l’étude générale des structures mathématiques, un domaine très abstrait des maths – dont je n’avais jamais entendu parler auparavant, et qui touche vraiment à la limite de ce que je crois comprendre. Que Galois et Corty s’y sentent comme des poissons dans l’eau, tant mieux pour eux ; mais j’espère au moins, lecteurs, qui vous êtes aussi un peu perdus… sinon je me sentirais vraiment seul.

– Bravo, Maître !

Gna gna gna. Quel fayot, ce Corty.

– Votre formulation nous apporte, de plus, un éclairage sur ce que nous avions appelé l’équivalence conceptuelle. Quand un treillis n’est pas un treillis de concepts subjectifs, si deux éléments peuvent être reliés via l’un des endomorphismes dont vous avez parlé, alors ils sont conceptuellement équivalents. Nous pouvons regrouper les éléments du treillis en classes, où tous les éléments de chaque classe peuvent être reliés via ces endomorphismes. Nous obtenons à la fin une partition du treillis, où chaque élément du treillis appartient à une classe et une seul, et où tous les éléments d’une classe sont conceptuellement équivalents. Nous pouvons alors fusionner tous les éléments d’un même ensemble, et ce qui reste, ce sont les concepts sous-jacents ! Cela nous indique que derrière n’importe quel treillis se cache un treillis de concepts subjectifs, que nous pourrions retrouver. Même si, dans bien des cas, le résultat offre peu d’intérêt, comme nous l’avons vu avec la pauvre pyrite.

– C’est une bonne idée, dit Galois, mais il faudrait la modifier un peu. A chaque fois que nous rangeons deux éléments non comparables du treillis dans une même classe, nous renonçons à l’idée qu’ils désignent deux concepts différents ; nous devons donc éliminer de la définition la ligne qui les concerne. Nous devons alors considérer valides les endomorphismes qui ne rendent pas leurs images incomparables, tout en préservant les autres éléments incomparables. Ceci peut nous amener à modifier et fusionner encore plus nos classes. Mais, je suis d’accord avec vous, ce processus se termine, et à la fin je pense que nous obtiendrons un treillis de concepts subjectifs.

– Je vois. Quelque chose comme ceci, proposa Corty :

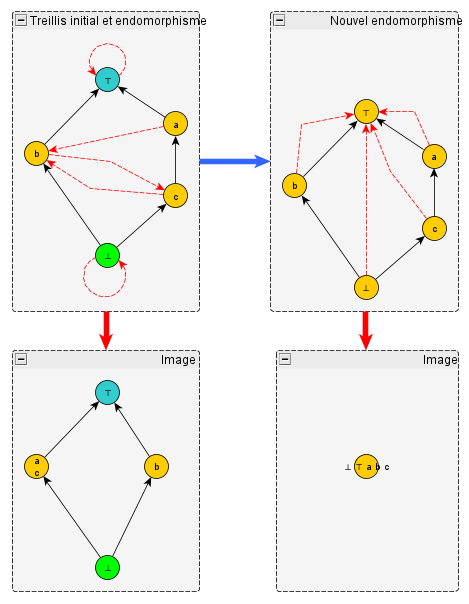
– À gauche nous avons un treillis avec un premier endomorphisme qui fusionne a et c en b et amène b en c, en gardant les deux autres éléments inchangés. En-dessous je montre ce que deviens le treillis si nous appliquons cet endomorphisme, en affectant le nom de chaque élément à son image. Les images de a et b, ainsi que celles de b et c, sont bien incomparables. Nous pouvons donc ranger a, b et c dans la même classe, les deux autres éléments restant chacun dans la sienne. Mais ce faisant, nous abandonnons la condition qui impose que les images de a et b ou b et c soient incomparables. Nous pouvons alors appliquer (à droite) un autre endomorphisme initialement interdit, qui fusionne tous les éléments en un seul. Nous trouvons bien que tous les éléments de ce treillis sont équivalents, et ne représentent qu’un seul concept.

– C’est cela. Formellement, il faudrait encore prouver que ce processus donne le même résultat quel que soit l’ordre dans lequel nous l’exécutons, et que le résultat est toujours un treillis ; mais (Galois se tourna vers moi en souriant) j’ai l’impression que nous avons fait assez de maths pour le moment. D’autant que nous avons bien d’autres questions passionnantes et moins techniques à aborder.

– Lesquelles, Maître ? demandai-je plein d’espoir.

– Nous avons atteint une bien meilleure compréhension de ce que sont les concepts subjectifs et de leur organisation en treillis, en ne nous appuyant que sur quelques règles issues de notre intuition. C’est bien, bravo à tous. Mais ce que nous ne savons pas encore du tout, c’est ce que ces concepts signifient pour une conscience. Qu’est-ce que ça fait, subjectivement, d’avoir ces concepts ? Que disent-ils, qu’expriment-ils ? Je pense, par exemple, au petit treillis de concepts subjectifs que nous avons utilisé dans nos discussions.

– Celui-ci ? écrivit Corty.

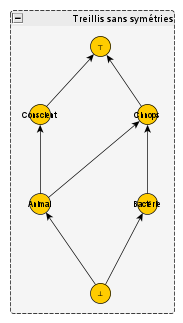
– Exactement. C’est le plus simple possible (si on ne considère pas le treillis à un seul élément, qui compte techniquement mais n’a aucun sens puisque rien y est tout). Mais que signifie ce treillis ? Clairement, il ne parle pas d’animal ni de chnops ni de quoi que ce soit d’aussi précis. Je veux bien conserver Rien et Quelque chose, mais les quatre autres noms… il nous faut les oublier, et nous poser la question : quel nom le plus général possible pourrions-nous donner à chaque concept de ce treillis ? Par ailleurs, j’ai toujours cette impression que nous avons manqué quelque chose d’important quand nous avons joué avec les treillis de Galois ; nous avons résolu notre problème de concepts « en trop », mais j’ai toujours le sentiment qu’il nous manque des concepts. Ceci dit… je n’ai pas la moindre idée de ce que cela implique ni de ce que nous devrions faire maintenant.

– Et moi non plus, soupira Corty.

Un long silence s’installa.

Ils se tournèrent tous deux vers moi. Ne me demandez pas comment Corty s’y prit, mais je vous assure que se sentir scruté par son propre cortex visuel est très intimidant.

– Euh… je suppose que nous devrions chercher un angle d’attaque différent…, balbutiai-je, avant de me réveiller en sursaut (et lâchement soulagé). Le ding d’un mail m’avait tiré du sommeil juste au bon moment. C’était Abel. Un mail d’une ligne :

Connecte-toi. C’est important. Sima veut te parler.

(à suivre)