
Le temps a filé, lectrice, et j’ai un peu perdu le fil de ma narration. Au reste, il ne se passa pas grand-chose cet été sur le front de ces recherches ; tout le monde était en vacances semble-t-il, consciences partielles, artificielles et oniriques comprises.
Je reçus cependant courant août une lettre à l’en-tête de l’hôtel Aleph ainsi libellée :
Mon bien cher ami,
J’interromps un instant mon délicieux séjour dans le tonneau de Diogène (que je vous recommande par ailleurs, l’air y est très sain) pour vous faire part de ma consternation. En effet, lors de nos derniers échanges, je me suis vu quelque peu emporter par un enthousiasme certes louable mais que ma fatigue de fin d’année universitaire m’a empêché de tempérer comme il l’eût fallu. En conséquence, j’ai commis une grave erreur dont je prends l’entière responsabilité et pour laquelle je vous prie humblement d’accepter mes sincères excuses.
Je vous ai en effet suggéré d’ajouter un nouveau treillis, appelé treillis d’expérience, en tant que support des concepts effectivement mémorisés ou inventés par Delta. Je ne reviens pas sur cette idée. En revanche, il est erroné de considérer que ce treillis est distinct du treillis subjectif de Delta : en effet, ces deux treillis n’en font qu’un.
Nous le savons, le treillis objectif, celui qui contient tous les percepts et concepts qui pourraient théoriquement exister dans le monde de Delta, est terriblement symétrique. A lui seul, il ne pourrait donc autoriser l’existence d’aucun concept subjectif, car tous les concepts qu’il contient, isomorphes ou redondants les uns avec les autres, seraient réduits à un seul. La seule caractéristique de Delta qui autorise l’émergence de concepts subjectifs, c’est au contraire le fait que son expérience est asymétrique. Certains percepts et concepts n’existeront pas dans l’esprit de Delta soit parce que la physique de son monde les interdit en pratique, soit parce qu’elle ne les rencontrera jamais, ou soit encore parce que, inutiles, ils seront oubliés voire jamais considérés. C’est uniquement dans ce cadre que les concepts subjectifs, nourris d’asymétrie, peuvent exister ; et ce cadre, c’est justement l’expérience de Delta. En d’autres termes, parler de treillis subjectif ou de treillis d’expérience comme de deux objets distincts n’offre guère de sens et il me semble naturel d’unifier les deux termes. Le treillis subjectif de Delta, c’est simplement le treillis qui contient tous les concepts rencontrés ou établis par Delta, réduits à leur forme irréductible qui élimine doublons et redondances ; c’est purement et simplement le support de ses états mentaux et de son expérience.
J’espère que cette correction, quoique tardive, vous aidera. Pour le reste, je ne puis actuellement consacrer à cette étude le temps qu’elle mérite, mais j’espère que vous arriverez à démêler, dans notre scénario de « l’invention du triangle bleu », les causes profondes qui conduisent Delta à calculer parfois la conjonction, parfois la disjonction de deux concepts.
Bien amicalement, votre dévoué
Evariste Galois.
Bien. Si l’on met de côté ses délicieuses formules surannées et son exquise gentillesse, la vérité nue est que Galois me refile le bébé encore une fois.
Regrouper le treillis d’expérience et le treillis subjectif, bien sûr, cela m’arrange et d’ailleurs ça tombe sous le sens ; les concepts subjectifs ne peuvent être construits que par l’expérience que l’on a du monde, et cette expérience elle-même est par définition subjective. Je m’en veux de ne pas y avoir pensé moi-même.
Cependant, tout cela ne réglait en rien l’autre problème : qu’est-ce qui pousse Delta à penser un coup à la disjonction de deux concepts – comme quand elle pense à un « triangle vert bon à manger » et qu’elle voit un délicieux triangle jaune – et un coup à leur conjonction – comme quand elle invente le fameux « triangle bleu » qui pourtant n’existe pas dans son monde – à part elle-même, comme me l’a rappelé Sima ? Il n’y pas vraiment de raison de privilégier l’un ou l’autre calcul. Nos scénarios sont trop ad-hoc, donc nécessairement incomplets, voire totalement faux.
C’est ici qu’intervient mon petit-fils Mica, charmant garçonnet composite venu passer un court séjour chez nous, et dont je me m’empresse de protéger la vie privée en lui inventant un prénom et en ne donnant aucun détail. Il suffira de savoir que, soit dit en toute objectivité et sans aucune gagaterie malvenue, il s’agit d’un enfant extrêmement attachant, curieux, intelligent, joli comme tout, et physiquement actif. Très actif, en fait.
J’avais laissé traîner l’un des nombreux dessins de treillis imprimé sur papier pelure, du genre de ceux que je vous ai déjà infligés ad nauseam, une des variations sur le Songe d’Everett qui servent de support à ma réflexion.
N’ayant pas les talents de Sima, j’utilise un logiciel libre de graphes et, je l’admets volontiers, le résultat est moche ; mais pour gamberger c’est pratique. Ce dessin, donc, en voici un exemplaire:
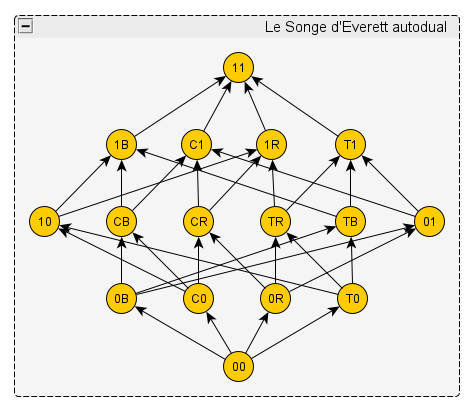
Dans cette variante du Songe d’Everett, j’avais déplacé quelques concepts par souci de symétrie. Par exemple, le concept « objet blanc » y est symétrique du concept « couleur blanche » par rapport à l’axe horizontal.
Je le retrouvai par terre, soigneusement plié en deux et agrémenté d’antennes du meilleur effet, avec une charmante dédicace :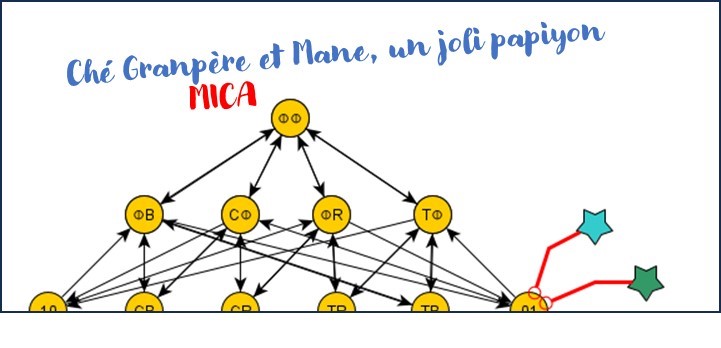 Comme vous le voyez, Mica avait plié le treillis au milieu des percepts et méticuleusement replié les ailes de son papiyon, de sorte que, par transparence, chaque concept de l’aile droite recouvrait un concept de l’aile gauche. Le concept « triangle de couleur quelconque » (T1), par exemple, recouvrait le concept « forme triangle » (T0); en transparence le zéro de « rien » et le 1 de « tout » s’y superposent en ce drôle de symbole, ⦶. Le concept « quelque chose » (11) et le concept « impossible » (00) sont également confondus. Vous noterez que quand deux concepts se recouvrent, les flèches qui les relient aux autres se recouvrent aussi la plupart du temps ; par transparence on obtient des flèches à deux têtes.
Comme vous le voyez, Mica avait plié le treillis au milieu des percepts et méticuleusement replié les ailes de son papiyon, de sorte que, par transparence, chaque concept de l’aile droite recouvrait un concept de l’aile gauche. Le concept « triangle de couleur quelconque » (T1), par exemple, recouvrait le concept « forme triangle » (T0); en transparence le zéro de « rien » et le 1 de « tout » s’y superposent en ce drôle de symbole, ⦶. Le concept « quelque chose » (11) et le concept « impossible » (00) sont également confondus. Vous noterez que quand deux concepts se recouvrent, les flèches qui les relient aux autres se recouvrent aussi la plupart du temps ; par transparence on obtient des flèches à deux têtes.
J’éprouvai un choc. Il y avait là une idée, presque à portée de main.
Si Mica a pu créer son joli papiyon bien symétrique, c’est parce que le treillis objectif que représente le Songe d’Everett est autodual – souvenez-vous, cela veut dire qu’on peut retourner le treillis et en obtenir un autre identique aux noms près. C’est un sujet que nous avions longuement discuté, mais que j’avais totalement laissé tomber par la suite. Ne devrait-on pas y revenir ?
D’abord, élaborer un peu cette nouvelle visualisation du treillis. Dans le papiyon de Mica, presque chaque concept sur l’aile droite recouvre son dual placé sur l’aile gauche. Les percepts, eux, sont pliés en deux, une moitié sur chaque aile, mais ça marche aussi car un percept est son propre dual.
Il reste tout de même deux concepts duaux qui ne se recouvrent pas : la forme (10) et la couleur (01) ; peut-on arranger ça ?
Après quelques tâtonnements j’ai obtenu ceci (sans antennes):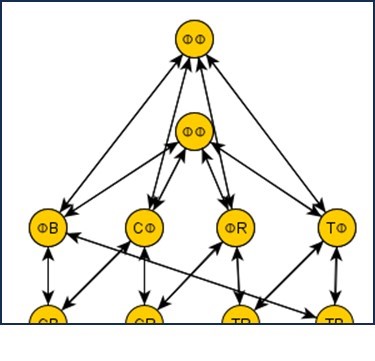 C’est bien moins joli certes, mais cette fois tous les couples de concepts duaux se recouvrent, et toutes les flèches sont devenues bidirectionnelles. Vous remarquez peut-être que le cercle du haut et celui en dessous de lui paraissent identique, mais en fait il n’en est rien : ce dernier est la superposition du concept « quelque chose » (11) et de son dual « impossible » (00), tandis que le premier est la superposition des concepts duaux « forme » (10) et « couleur » (01).
C’est bien moins joli certes, mais cette fois tous les couples de concepts duaux se recouvrent, et toutes les flèches sont devenues bidirectionnelles. Vous remarquez peut-être que le cercle du haut et celui en dessous de lui paraissent identique, mais en fait il n’en est rien : ce dernier est la superposition du concept « quelque chose » (11) et de son dual « impossible » (00), tandis que le premier est la superposition des concepts duaux « forme » (10) et « couleur » (01).
Ce que nous avons ici, ce n’est certes pas un treillis. Il n’y a plus d’élément minimal ou maximal unique, et les flèches partent dans les deux sens.
D’un autre côté, c’est juste un treillis replié, n’est-ce pas ? J’ai toujours le choix de le déplier à nouveau et j’obtiendrai un treillis parfaitement légal.
Ce qui m’intéresse ici, c’est que si on superpose les concepts duaux, alors la différence entre conjonction et disjonction s’amenuise un peu. Je m’explique. Regardons l’aile droite. On y voit (à moitié) les concepts « triangle bleu » (TB) et « triangle rouge » (TR). Leur disjonction, c’est « triangle de couleur quelconque » (T1), qui est également dessiné sur l’aile droite. Mais leur conjonction, les propriétés qu’ils ont en commun, c’est « forme triangle » (T0), qui est justement le dual du précédent, placé sur l’aile gauche. Si je marque la disjonction des deux concepts sur l’aile droite, en retournant le papiyon je vois leur conjonction sur l’aile gauche.
Cela marche-t ’il aussi pour d’autres concepts ? La conjonction de « triangle de couleur » (T1) et « objet rouge » (1R), qui sont tous deux sur l’aile droite, c’est « triangle rouge » (TR), qui est aussi sur l’aile droite (et sur la gauche). Leur disjonction c’est … n’importe quoi (11). Zut, ce deux concepts ne sont pas dans le même cercle. Ah mais attendez. Il faut d’abord retourner le papiyon. Le dual de « triangle de couleur », c’est « forme triangle » (T0). Celui de « objet rouge », c’est « couleur rouge » (0R), qui apparaissent tous deux sur l’aile gauche. La disjonction de ces deux-là, c’est aussi « triangle rouge », qui est son propre dual et apparaît à cheval sur les deux ailes.
En d’autres termes, pour calculer la conjonction de deux concepts sur une aile, je peux retourner le papiyon, calculer la disjonction de leur concepts duaux sur l’autre aile, puis retourner à nouveau le papiyon et lire le concept dual de ce résultat. Ou encore : le dual d’une conjonction, c’est la disjonction des duaux, et réciproquement. En termes plus mathématiques, cela s’écrit :
(a ⋏ b)* = a* ⋎ b* et (a ⋎ b)* = a* ⋏ b*
et cela se prouve facilement. Dans un treillis autodual, il existe donc une jolie symétrie entre conjonction et disjonction. Or, non seulement le treillis objectif de Delta est autodual, mais son treillis subjectif l’est aussi, du moins à en croire le Caillou dont les arguments me semblent convaincants. Par ailleurs, ce treillis subjectif, il semble que Delta l’enrichisse en comparant les percepts qu’elle rencontre avec d’autres concepts déjà existants. Si nous voulons que le treillis subjectif reste autodual, il faudrait donc que chaque fois que Delta y ajoute un concept, elle y ajoute également son dual ; et que chaque fois qu’elle en oublie un, elle oublie son dual avec.
Poussons cette symétrie un peu plus plus loin. Je décrète que quand delta pense à un concept subjectif, elle pense aussi à son dual.
Dans les scénarios que nous avons discutés ave Galois, Delta découvre (ou invente) des concepts en comparants les percepts qu’elle rencontre avec les concepts auxquels elle pense. De manière plus générale, quand Delta perçoit ou pense à des concepts, elle va les comparer deux à deux et en fabriquer de nouveaux. Disons que pour comparer deux concepts, Delta calcule leur disjonction, ce qui lui permet de filtrer la situation actuelle par rapport à son intérêt du moment. Elle va donc calculer la disjonction de toutes les paires de concepts impliqués. Mais comme penser à un concept implique de penser à son dual, comme je l’ai imposé, Delta va aussi calculer la disjonction de chacun d’eux avec le dual de l’autre, ainsi que celle des deux concepts duaux. Enfin, pour faire bonne mesure, elle calcule le dual de chaque concept obtenu. Tout cela nous donne de nouveaux concepts (ou bien sûr des concepts déjà existants), avec l’assurance dans tous les cas que chaque nouveau concept arrive avec son dual.
Par exemple, si Delta rencontre un triangle jaune puis un triangle vert, tous deux bons à manger, elle calculera leur disjonction, qui est le concept « triangle de couleur, bon à manger ». Elle calculera ensuite le dual de ce dernier, qui est « forme triangle, bon à manger », et qui se trouve également être la conjonction des deux percepts.
De même, quand Delta invente le triangle bleu, c’est parce qu’elle pense en même temps à « triangle de couleur délicieux » et « objet bleu délicieux ». En calculant leur disjonction elle obtient « objet de couleur, délicieux », dont elle calcule aussi le dual « sensation de délice ». Mais elle calcule également la disjonction de leurs concept duaux respectifs, à savoir « forme triangle délicieux » et « couleur bleue délicieuse ». Cette disjonction n’est autre que le fameux « triangle bleu délicieux » ! Delta effectue encore deux autres calculs moins utiles ; par exemple elle calcule la disjonction de « triangle de couleur délicieux » et de « couleur bleue délicieuse », qui est juste « triangle de couleur délicieux ». Au total, cependant, Delta créera trois nouveaux concepts : « objet de couleur délicieux », « sensation de délice » (dual du précédent) et enfin « triangle bleu délicieux » (qui est bien sûr son propre dual).
Le fait que j’ai choisi de toujours calculer la disjonction de deux concepts pour les compare n’a aucune importance. J’aurais pu décider de calculer leur conjonction et j’aurais obtenu exactement le même résultat. Ce qui compte c’est que le dual de chaque concept soit aussi pris en compte dans les calculs. En fait, dans un treillis autodual, la conjonction se calcule automatiquement à partir de la disjonction et de la dualité; ces deux opérations suffisent et nous n’avons plus besoin de la troisième.
Je me sentis plutôt fier de moi, jusqu’au moment ou Corty – qui n’avait pas donné signe de vie depuis un moment – intervint :
– C’est pas mal tout ça, assez convaincant même, mais il y a un truc qui me gêne. Si on pense toujours au dual d’un concept auquel on pense, alors comment faire la différence entre les deux ? Si tu penses toujours « objet bleu » et « couleur bleue » exactement en même temps, je ne vois vraiment pas comment tu peux distinguer ces deux concepts. Subjectivement, ils n’en forment qu’un, non ? Autrement dit, tu ne peux pas vraiment déplier le papiyon en esprit. Si un concept subjectif et son dual sont en fait la même chose, ce n’est plus un treillis que tu manipules : c’est le papyion lui-même, dans lequel chaque concept et son dual se confondent en un seul cercle vu en transparence, et c’est ce cercle qui est le concept subjectif. Si on va par là, tout notre travail sur les treillis est à mettre à la poubelle. Attention, je ne dis pas que c’est absurde, je dis juste que si c’est vrai tu viens de nous rajouter quelques mois de boulot.
Je hochai sombrement la tête. Pourvu que Galois revienne vite.
(à suivre)









0 commentaires