Je donne ici la parole à mon vieux copain Thierry Banel, avec qui nous avons partagé en nos vertes années la même passion pour l’Intelligence Artificielle et, la maturité venant, la même conviction que les maths ont leur mot à dire quant aux évolutions de notre société. Cette chronique fera donc pour l’essentiel appel à un court texte envoyé par Thierry à ma compagne et à moi-même, que je me contente de remettre en forme en y ajoutant quelques références et notes de contexte.

Comme vous le constaterez, Thierry pousse en l’occurrence le concept à sa limite. Je ne sais ce qu’il y a de plus glaçant dans cette analyse : sa concision, la force expressive sans appel des graphiques, la froideur apparente du langage mathématique appliqué à ce qui nous est le plus précieux – la survie même de notre civilisation ? Ou plutôt le fait que, visiblement, presque tout le monde s’en fiche et que l’on continue à nous servir des fadaises sur une croissance éternelle qui ressemble de plus en plus à l’escalier d’Escher ?

Je laisse à vous le soin d’en juger, et à Thierry la parole. Bonne lecture.

Yannick Cras

***

Il y a quelques années la NASA a publié une petite étude basée sur un modèle de civilisation simplifié. Le modèle s’appelle Handy. Il fait varier les populations de prédateurs et de proies [1].

Lotka – Volterra equations

Dans ce modèle simpliste ils ont ajouté une stratification sociale: des travailleurs et une élite. Les travailleurs produisent les richesses, et l’élite les confisque, laissant aux travailleurs juste de quoi survivre. Puis ils l’ont fait tourner :

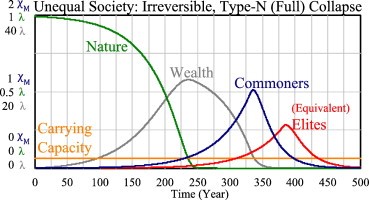
Ils ont observé des effondrements civilisationnels. En faisant varier les paramètres, on obtient différents effondrements. Quelques paramètres très bien ajustés peuvent donner une civilisation stable. Mais le plus souvent elle s’effondre.

Ce modèle simpliste, dit la publication, est en accord avec des données historiques : l’empire romain, la civilisation mycénienne, sumérienne, mésopotamienne, l’empire khmer, les Hans, les Mayas, etc. Tous ces empires se sont effondrés. L’étude explique que la stratification en classes sociales est un élément clé des effondrements.

Dans le même ordre d’idées, le modèle civilisationnel dynamique World3 a été commandé par le Club de Rome dans les années 1970. Il a été perfectionné depuis. Il contient toutes sortes de variables : production, terres arables, espérance de vie, accumulation de richesses, etc. qui interagissent entre elles.

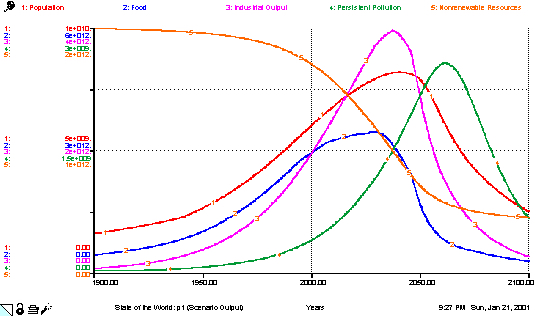
Les auteurs, très fiers de leur modèle, ont introduit les données réelles du monde des années 70. Ils ont appuyé sur la touche « enter », car la souris n’avait pas encore été inventée. Les variables sont parties en croissance exponentielle, puis tout s’est effondré.

Ils ont fait la tronche. Puis ils ont eu l’idée de faire varier les paramètres 
– Productivité agricole fois deux, enter, effondrement.
– Gros efforts de dépollution, enter, effondrement.
– Meilleurs hôpitaux, enter, effondrement.
– etc.

Au bout d’un moment, en tripotant tous les paramètres, ils ont fini par trouver une civilisation à peu près stable dans le temps. C’est le modèle qu’ils ont préconisé dans leur rapport au Club de Rome.

À ces modèles et bien d’autres études historiques est venu s’ajouter la notion de pic pétrolier. C’est la date où la production mondiale de pétrole atteint son apogée. Certaines études le situent en 2006 : nous l’aurions donc dépassé. Nous serions sur le déclin de notre civilisation basée sur le pétrole. Il y a aussi l’épuisement des mines de terres rares (métaux précieux comme le lithium ou le niobium), le dérèglement climatique qui crée des déserts et provoque la mort de tas d’espèces vivantes, la destruction des abeilles par les néonicotinoïdes, donc la fin de la pollinisation, la montée des inégalités de richesses, les migrants climatiques, économiques, et de guerre, la croissance du PIB comme seul critère de politiques publiques.

Tout indique que le mythe du progrès linéaire est une illusion…

Thierry Banel
Le nombre imaginaire

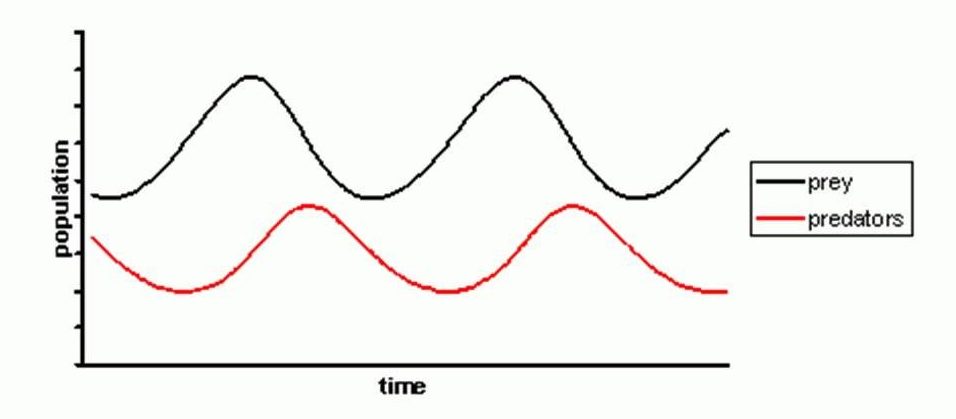
[1]  Les modèles mathématiques étudiant l’évolution de populations de proies et de leurs prédateurs forment un exemple assez classique de boucle de rétroaction, régi par les lois dites de Lotka-Volterra. Plus la population de prédateurs est grande, plus la population de proies diminue, ce qui entraine une raréfaction des ressources alimentaires disponibles aux prédateurs, qui elle-même entraine une baisse de leur population et donc une nouvelle poussée de population des proies (YC).