Le lendemain soir, j’eus grand-mal à m’endormir eu égard à l’excitation que m’avaient donné cette première discussion avec Galois et sa retranscription au réveil ; cependant je finis par me retrouver dans son bureau encombré et poussiéreux de la rue d’Ulm, où traînaient entassés pamphlets révolutionnaires et traités de mathématiques.

Il m’accueillit d’un signe de tête distrait, déjà affairé à son tableau noir où s’estompaient d’étranges dessins, comme des filets de pêcheur.

– Vous êtes en retard.

– Vous m’en voyez confus!

– Ce n’est pas si grave, j’ai avancé sans vous. Bien. Continuons d’explorer votre ensemble de concepts, car il présente à mon avis d’autres propriétés intéressantes. Etant donnés deux concepts, il me semble qu’il devrait toujours exister un concept représentant les exemples qu’ils ont en commun. Qu’en pensez-vous ?

– Je suis d’accord. Tout ce qui est pensable est un concept ; or je peux clairement penser aux exemples communs à deux concepts. Par exemple, à partir du concept de triangle et du concept de forme rouge, je peux définir le concept de triangle rouge, comme nous en parlions hier. Je trouverais logique d’étendre cette possibilité à tous les couples de concepts.

– Parfait. Nous définissons donc une opération qui, à partir de deux concepts a et b, en détermine un troisième c. Je vais la noter ainsi :

a ⋏ b = c

Nous pourrions appeler cette opération conjonction de a et b, puisque a ⋏ b représente le concept de ce qui ressort à la fois des concepts a et b. Que vous dit votre intuition sur cette opération ?

– Hmmm… Déjà, on peut échanger les deux concepts sans changer le résultat. Un triangle rouge, c’est comme un rouge triangle, si je puis dire.

– Absolument. L’opération est dite commutative :

∀(a,b) ∈ C², a ⋏ b  = b ⋏ a.

Dans la même veine, notre opération est également associative : on peut l’étendre à plus de deux concepts, et le résultat du calcul ne dépend pas de l’ordre dans lequel on les prend. Par exemple, un « grand triangle » rouge est aussi un grand « triangle rouge », si je puis me permettre ce jeu de langage. Voici la formule correspondante :

∀(a,b,c) ∈ C³, ( a ⋏ b ) ⋏ c  = a ⋏ (b ⋏ c).

Voyez-vous autre chose ?

– Hmmm… Ah, oui : la conjonction d’un concept avec lui-même, c’est lui-même. Un « triangle triangle », c’est tout bêtement un triangle.

– Absolument. Je l’écris :

∀ a ∈ C, a ⋏ a = a.

Cette propriété s’appelle l’idempotence.

– Je pense même à une propriété plus générale : si a spécialise b, alors la conjonction de a et b, c’est a. Comme il se spécialise aussi lui-même, a est bien le concept le plus général qui spécialise les deux. Une « forme triangle », c’est un triangle.

– Très bien ! Voici la formule :

∀(a,b) ∈ C², a ≼  b ⇒ (a ⋏ b =  a).

Remarquez d’ailleurs que la réciproque est vraie, car nous voulons bien sûr que a ⋏ b spécialise à la fois a et b. De ce fait, si a ⋏ b = a, alors a ≼ b. En combinant ces deux affirmations, on déduit que a spécialise b si et seulement si la conjonction de a et b est égale à a, ce qui s’écrit

∀(a,b) ∈ C², a ≼  b ⇔ (a ⋏ b =  a).

C’est intéressant : nous avons défini l’opération de conjonction ⋏ à partir de l’ordre de généralisation ≼, mais nous aurions pu faire l’inverse.

– Oui… mais je me pose une question. Nous savons que a ⋏ b spécialise a et b, mais que se passerait-il si un autre concept les spécialisait aussi, et qu’il soit plus général que a ⋏ b ?

– Cela n’irait pas. L’idée est bien que a ⋏ b soit le concept le plus général qui spécialise à la fois a et b. Par exemple, le concept [panneau « laisser le passage »] spécialise bien les concepts [triangle] et [forme rouge], mais il est moins général que le concept [triangle rouge]. Heureusement, sur la base des propriétés que nous avons imposées à l’opération de conjonction, nous pouvons prouver que a ⋏ b est bien le concept le plus général qui spécialise à la fois a et b. Voulez-vous essayer de le faire ?

– Hmmm… supposons qu’un concept c spécialise à la fois a et b. Nous devons montrer que c spécialise aussi a ⋏ b. Ainsi, nous saurons que ce dernier est bien le concept le plus général qui spécialise a et b. Voyons voir. Si c ≼ a, alors c ⋏ a = c ; de même comme c ≼ b, c ⋏ b = c. Donc, grâce à la propriété d’associativité que nous avons imposée,  c ⋏ (a ⋏ b) = (c ⋏ a) ⋏ b  = c ⋏ b = c. Donc c ⋏ (a ⋏ b) = c et on en déduit que c ≼ (a ⋏ b). Ça marche !

– Très bonne démonstration, bravo.

– Merci… mais il reste un problème, me semble-t-il.

– Lequel ?

– Eh bien, qu’est-ce qui nous prouve que a ⋏ b est toujours unique ? Pour deux concepts a et b, nous pourrions a priori avoir deux concepts x et y qui respecteraient tous les deux les conditions précédentes. Lequel choisir dans ce cas ?

– Excellente question. Fixons deux concepts a et b. Si deux concepts x et y sont candidats au rôle de a ⋏ b, alors ils respectent tous deux les conditions que nous avons établies, et donc :

∀c ∈ C, ( c ≼ a) ∧ (c ≼ b ) ⇒ c  ≤  x.
∀c ∈ C, ( c ≼ a) ∧ (c ≼ b ) ⇒ c  ≤  y.

Maintenant, vu que y spécialise bien à la fois a et b, je peux l’utiliser à la place de la variable c dans la première formule, et j’en déduis que y ≼  x. Mais je peux aussi, de la même manière, remplacer c par x dans la deuxième formule, et j’en déduis que x ≼  y. Au total, x = y. Pour deux concepts a et b donnés, il n’y a qu’un seul concept qui respecte les conditions que nous avons fixées pour a ⋏ b ; ce dernier est donc unique.

– Me voilà rassuré… à moitié seulement. Si a ⋏ b existe, il est unique ; mais comment pouvons-nous être sûrs qu’il existe toujours ?

– Mais parce que nous l’avons décidé, tout simplement ! Pour tout couple de concepts, notre intuition impose l’existence d’un concept unique, le plus général possible et qui les spécialise tous deux. Nous avons le droit de dire ça. Nous devons juste vérifier que cela n’amène pas d’absurdités et qu’il existe réellement des exemples intéressants d’ensembles de concepts ayant ces propriétés. Si les conditions que nous imposons nous amenaient à prouver, par exemple, que tous les concepts sont identiques, alors nous saurions que nous faisons fausse route. Je vous promets que ce n’est pas le cas jusqu’ici.

– Vous me rassurez. Mais dites-moi, je pense à quelque chose. Ne pourrait-on pas définir une autre opération sur les concepts ? Une sorte d’inverse de la conjonction. Il me semble que, étant donné deux concepts, il en existe toujours un qui les généralise tous les deux. Par exemple, un triangle rouge et un triangle bleu sont tous deux des triangles. Qu’en pensez-vous ?

– C’est une bonne idée ! Nous pouvons décréter que, étant donnés deux concepts a et b, il existe un concept qui généralise a et b, et qui est le plus spécifique possible ; nous le noterons a ⋎ b, ou disjonction de a et b.  Pour reprendre votre exemple, j’écrirai :

 [triangle rouge] ⋎ [triangle bleu] = [triangle]

En fait, à y réfléchir, cette nouvelle opération a exactement les mêmes propriétés que l’autre si on inverse les mots « spécialise » et « généralise ». Par exemple, a ≼ b ⇔ (a ⋎ b = b) ; l’opération ⋎ est aussi associative, commutative et idempotente. Enfin, nous pouvons prouver que a ⋎ b est l’unique concept qui généralise a et b et qui est le plus spécifique de tous.

– Vous dites que nous avons imposé l’existence de a ⋏ b, et maintenant de a ⋎ b. Est-ce qu’on n’aurait pas pu les prouver plutôt, à partir des propriétés que nous avions établies hier ?

– Non. Ces nouvelles conditions que nous imposons, comme l’existence de a ⋏ b, ne sont en rien évidentes dans le cas général d’un ensemble partiellement ordonné.  Par exemple, imaginons pour un instant que C soit un ensemble de personnes, et que la relation a ≼ b veuille dire « a est un descendant de b (ou b lui-même) ». C resterait un ensemble partiellement ordonné avec toutes les propriétés qui conviennent. Comment appelle-t-on quelqu’un qui descend de deux personnes données, et dont aucun ascendant n’a cette propriété ?

– Un de leurs enfants, tout bêtement. Sauf si l’une des personnes descend de l’autre.

– Eh oui. Or rien n’impose qu’un couple de personnes quelconques ait des enfants, ou qu’ils n’en aient qu’un seul. Deux frères et sœurs partagent les mêmes parents et ne sont pas descendants l’un de l’autre. Il est impossible de définir a ⋏ b dans ce cas.

– L’ensemble des concepts n’est donc pas n’importe quel ensemble partiellement ordonné. Il a des propriétés additionnelles, comme l’existence de a ⋏ b et a ⋎ b. De tels ensembles ont-ils un nom ?

 – Oui. Nous avons de la chance : il s’agit d’une structure mathématique connue, qui s’appelle un treillis fini. Elle a été étudiée dans le détail, et présente des caractéristiques très intéressantes.

– Par exemple ?

– Par exemple, revenons aux concepts minimaux dont nous avons parlé hier, ceux qui n’ont aucune spécialisation à part eux-mêmes. Nous avons vu qu’il en existe nécessairement. Prenons-en deux au hasard, disons m et n. Que pensez-vous de m ⋏ n ?

– Euh… c’est étrange…

– En effet, c’est étrange. Car m ⋏ n est une spécialisation de m, lequel est minimal. Comme m n’a pas d’autre spécialisation que lui-même, cela implique que m ⋏ n = m.

– Mais pour la même raison, m ⋏ n = n. Cela veut dire que m et n sont le même concept !

– Voilà. Ce que nous venons de prouver, c’est que dans un treillis fini il n’existe qu’un seul concept minimal.

– C’est très bizarre !

– Pas tant que ça. Qu’est-ce qui est à la fois un triangle rouge et un carré bleu, par exemple ?

– Euh… mais rien !

– En effet, rien. Or le concept de « rien », ou peut-être « impossible », est un concept parfaitement pensable, non ? Et il spécialise tous les autres concepts. En effet, comme rien de concret n’est « rien », tout ce qui est « rien » est aussi n’importe quoi d’autre. Notre concept minimal, c’est ce concept « rien ». On le note souvent par ce symbole : ⊥. D’ailleurs, vous vous souvenez que, tout comme nous avons défini un concept minimal, nous pouvons définir un concept maximal ? C’est un concept qui n’a pas d’autre généralisation que lui-même.

– Oui, et il doit en exister au moins un dans un ensemble de concepts fini.

– Absolument. Vous ne serez peut-être pas surpris si je vous apprends que, dans un treillis, il est également unique…

– Laissez-moi deviner. C’est le concept de « tout », ou de « n’importe quoi », ou peut-être de « quelque chose » ?

– Exactement. J’aime bien ce dernier terme, en particulier. Tout ce qui existe est quelque chose. Un triangle est quelque chose, une forme rouge aussi. Ce « quelque chose » est représenté par le symbole ⊤.

– Il semble y avoir une belle symétrie à l’œuvre dans un treillis. Les deux concepts ⊥ et ⊤, les deux opérations ⋏ et ⋎…

– Absolument ; on parle ici de dualité. Les concepts [rien] et [quelque chose] sont duaux l’un de l’autre ; la conjonction et la disjonction sont duales l’une de l’autre. De fait il n’y a pas grand mystère à cela.

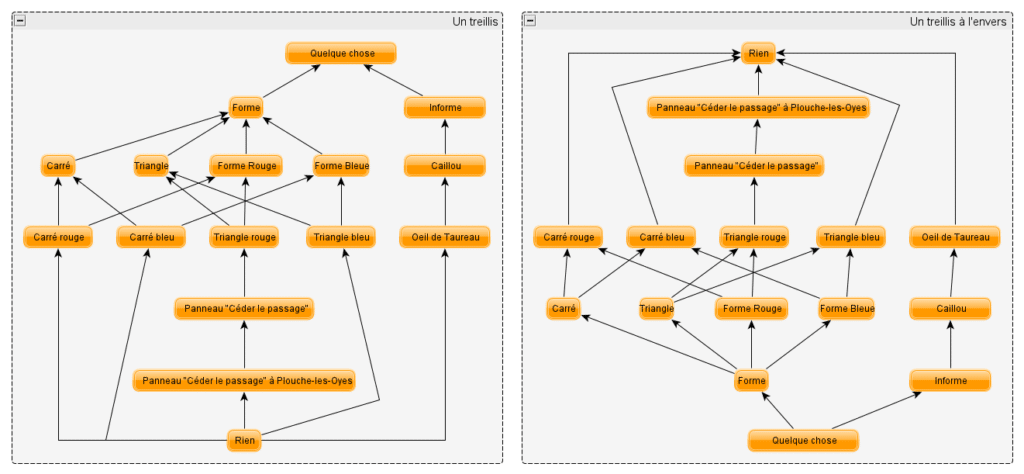
Tenez, je représente ici à gauche un treillis illustrant les exemples dont nous avons parlé (avec quelques concepts de plus pour faire bonne mesure). Vous y retrouverez nos concepts de rien et de quelque chose. Pour trouver la conjonction de deux éléments vous cherchez l’élément le plus haut placé qui est relié à chacun d’eux deux par un chemin de flèches. Pour trouver leur disjonction, vous cherchez l’élément le plus bas que l’on peut atteindre à partir de chacun des deux par un chemin de flèches.

Maintenant je dessine à côté le même treillis mais présenté à l’envers et dans lequel j’inverse le sens des flèches. J’obtiens également un treillis. Vous le voyez, ces deux treillis ont les mêmes éléments mais l’ordre y est inversé :  si a ≼ b dans le premier, alors b ≼ a dans le deuxième. On dit que chacun est le dual de l’autre. Le concept qui joue le rôle de l’élément minimal dans l’un est l’élément maximal de l’autre ; et vous remarquerez que si a ⋏ b = c dans un des treillis, alors a ⋎ b = c dans l’autre. La dualité est un concept puissant dans l’étude des treillis, et à mon avis nous devrions compter sur elle pour notre étude de la conscience. Mais je vois que vous allez vous réveiller. Je vous laisse y réfléchir, à bientôt !

– Hmmm…. C’est fascinant ! Merci, et à bientôt !

À suivre…