Je me suis retrouvé en rêve dans le bureau de Descartes, toujours aussi en fouillis. Il était assis face à son ordinateur mais, cette fois, en compagnie d’un très jeune homme pâle, distingué, magnifique en habit du plus bel effet – effet cependant quelque peu gâché par le trou de balle qui perforait sa veste sur le côté.

Descartes m’accueillit d’un signe de tête :

– Vous tombez fort bien, mon cher, car cela me donne l’occasion de vous présenter un jeune ami mathématicien de passage. Je lui ai touché un mot de votre projet qui a beaucoup éveillé son intérêt, n’est-ce pas Evariste ?

– Evariste… Evariste Galois ?

Je suis effaré. Il n’y a pourtant aucun doute. Evariste Galois, précoce génie des maths, républicain passionné et rebelle, tête brûlée volontaire dans la Garde Nationale, mort en 1832 à l’âge de vingt ans – stupidement abattu par un quelconque crétin lors d’un duel pour l’amour d’une jeune fille (« une infâme coquette » selon ses mots) dont j’espère in petto qu’elle aura tout de même au moins rendu ses derniers jours heureux. Quelle histoire. Quel gâchis. Sa courte vie lui aura pourtant suffi à livrer à la postérité des travaux précurseurs de l’étude moderne des structures mathématiques.

– C’est moi-même ; enchanté. René m’a parlé de vos travaux, c’est un sujet que je trouve intéressant. Avez-vous pu avancer ?

– Un peu, je crois… Mais je bute à présent sur une difficulté majeure. Je cherche à définir formellement la notion de concept, en tant que ce qui est pensable par un sujet conscient. J’en cherche la plus large définition possible, mais qui puisse être utile sur le plan mathématique.

– Hmmm… C’est un bon sujet. Comme vous le savez peut-être, je suis moi-même passionné par les relations qui lient des entités mathématiques distinctes, que je considère comme révélatrices de leur nature profonde.

– A ce que j’en ai compris, au lieu de chercher à calculer des solutions d’équations algébriques, vous avez cherché à identifier ce qui les relie, et les conditions que doit respecter l’équation pour que des solutions existent. Ce faisant, vous avez posé les fondations de l’algèbre moderne, qui s’intéresse à des structures mathématiques abstraites dont les éléments ont certains types de relations entre eux.

– Exactement. Il est regrettable que cet… incident (il désigne le trou dans sa veste) m’ait détourné de ce chemin que je pensais prometteur ; mais mes successeurs ont fait un formidable travail. Pour en revenir à votre sujet, je pense qu’une approche du même ordre pourrait être fructueuse. Tout d’abord, si votre sujet conscient manipule des entités appelées concepts, à quelles autres entités a-t-il accès ?

– Eh bien… comme je me suis persuadé que perception et pensée sont une seule et même chose, il semble bien que le concept (en tant que ce qui se perçoit ou se pense) soit le seul objet de ce modèle en gestation. C’est un problème ?

– Pas du tout. Cela circonscrit même la question. Pour caractériser ce qu’est un concept, vous devrez expliciter les relations qu’il entretient avec les autres objets du discours – en l’occurrence les autres concepts. Vous n’avez pas d’objet plus primitif qui puisse le constituer ou le définir ; mais ce n’est pas insoluble. Il y a de nombreux autres exemples en mathématiques. Par exemple, les entiers naturels sont définis en décrétant qu’il existe un entier appelé zéro, et que tout entier est associé à un entier appelé son successeur, différent de lui-même et du successeur de tout autre. Pour définir les nombres entiers vous n’utilisez donc que des relations entre nombres entiers, et ça ne gêne personne. Il existe d’ailleurs un outil mathématique formidable, très abstrait et puissant, développé au XXe siècle, qui s’appelle la théorie des catégories. Dans ce modèle, une entité n’est définie que par les relations qu’elle entretient avec les autres : vous voyez que vous êtes en bonne compagnie.

– Il me faudrait donc, pour définir ce terme de concept, expliciter les relations possibles entre concepts.

– Exactement. Vous pourriez commencer par me donner quelques exemples de concepts au sens que vous donnez à ce mot ?

– Hmmm… Eh bien, déjà, tous les mots du dictionnaire ; un chien, un chat, un lézard, une souris, un animal, tous les verbes comme manger, dormir… Et puis des concepts plus sensoriels, disons un ciel bleu, l’odeur des roses, une foulée rapide ; des concepts abstraits comme une famille, un triangle, Dieu, la conscience, le théorème de Pythagore, la 7^e symphonie de Beethoven ; des concepts très précis comme le caillou que j’ai dans ma poche ou le souvenir d’un coucher de soleil au Vert-Galant sur l’île de la Cité quand j’avais 16 ans… Ce genre de choses.

– C’est un début. Voyez-vous certains concepts comme plus simples, plus primitifs que d’autres ? Un peu comme le zéro des nombres entiers ?

– Hmmm… certains concepts sont plus abstraits, d’autres plus concrets. On pourrait peut-être définir un concept abstrait comme collection de concepts plus concrets ; par exemple le rouge est la couleur des cerises et celle du sang…

– C’est juste. Cependant, vous pourriez tout aussi bien définir un concept concret comme une conjonction de concept plus abstraits. Par exemple, une cerise est à la fois un fruit et quelque chose de rouge. Dans ce cas, c’est la cerise qui deviendrait un concept composé, et la couleur rouge un concept plus primitif.

– Vous avez raison, il me paraît difficile de trancher.

– Nous reviendrons sur ce point, car il m’évoque quelques idées. Mais revenons aux relations entre concepts. Quel type de relations pourrions-nous définir ?

– Eh bien, les objets concrets entretiennent de multiples relations. Par exemple, les chats mangent des souris.

– Oui, mais le concept de chat ne mange pas le concept de souris. Un concept n’a pas d’estomac que je sache. Ce serait comme dire que le mot « chat » mange le mot « souris ».

– C’est vrai. On pourrait, cependant, considérer le concept « manger » comme une relation : un exemple d’un certain concept, par exemple du concept « animal », mange un exemple d’un autre concept, disons le concept de « chose comestible ». Cela établirait une forme de relation entre ces trois concepts. D’ailleurs, en informatique… Vous connaissez ce terme ?

– Oui, Turing et d’autres m’en ont parlé.

– En informatique, donc, nous utilisons ce type de formalisme pour représenter des types de données.

– Je le comprends. Mais j’avais en tête une forme plus générale de relation entre concepts, quelque chose de plus fondamental. Une relation naturelle, simple et universelle qui puisse exister entre concepts indépendamment des relations spécifiques entre les objets concrets qu’ils désignent. D’ailleurs vous l’avez-vous-même évoquée, en parlant de concepts plus abstraits ou plus concrets que d’autres.

– Laquelle ?

– Verriez-vous un lien entre le concept de triangle et le concept de forme ?

– Euh… oui. Un triangle est une forme.

– Juste. Mais le concept de triangle n’est pas le concept de forme, pas plus que le mot « triangle » n’est le mot « forme ». En revanche, ces deux concepts sont tout de même liés par une relation particulière.

– L’un est plus général que l’autre. Tout exemple du concept de triangle, disons tout triangle concret, est aussi un exemple du concept de forme.

– Exactement, même s’il faudrait sans doute définir plus formellement ce que nous entendons par « exemple ». Quoi qu’il en soit, le concept de triangle coloré est plus général que le concept de triangle rouge, comme d’ailleurs le concept de forme rouge. Le concept d’animal est plus général que le concept de chien, lequel est plus général que le concept du chien Lassie, etc.

– En revanche, le concept de triangle coloré et le concept de forme rouge ne sont pas comparables en ce sens : aucun des deux n’est plus général que l’autre.

– En effet. Bien, nous disposons donc d’une relation générale entre concepts, que nous allons pouvoir étudier de plus près. René, puis-je utiliser votre tableau noir ?

Galois se lève et commence à griffonner sur le tableau.

– Nous allons commencer par choisir un nom pour l’ensemble des concepts que nous manipulons. Je propose de le noter C, en caractère gras, tout simplement. Au fait, cet ensemble serait-il par hasard fini, ou au moins dénombrable, à votre avis ? Cela nous simplifierait certainement la vie.

– Il faut le supposer fini, s’il vous plait. Ma récente discussion avec M. Descartes m’en a convaincu. Cela me permettra d’échapper aux arguments des dualistes (je vis Descartes froncer le sourcil, mais il s’abstint d’intervenir).

– Cela me convient parfaitement. Nous allons également supposer que C n’est pas vide et qu’il existe au moins un concept ; ça a l’air idiot, mais c’est important pour la validité de nos raisonnements. Bien, je vais ensuite noter le fait qu’un concept p (particulier) est moins général qu’un concept g (général) en écrivant

p ≼ g.

Nous pourrons aussi dire que g généralise p ou que p spécialise g. Vous le voyez, j’utilise des lettres minuscules pour désigner des concepts quelconques. Par ailleurs, quand nous utiliserons des exemples précis de concepts pour illustrer nos propos, je noterai leur nom entre crochets droits pour éviter toute ambiguïté. Par exemple, nous pouvons écrire (joignant le geste à la parole) :

[triangle rouge]≼ [triangle].

Bien, quelles sont à votre avis les propriétés que nous devrions attendre de cette relation ≼ ?

– En premier lieu, elle est réflexive. Tout concept se généralise lui-même, puisque tous ses exemples sont, euh, ses exemples.

Hochant la tête, Galois note au tableau la formule :

∀c ∈ C, c ≼ c.

– Bien commode, cette notation logique. Dommage qu’elle n’ait pas existé à mon époque. Ce A à l’envers pour dire « quel que soit », ce symbole ∈ pour dire qu’un élément appartient à un ensemble… c’est vraiment malin.

– Ne m’en parlez pas, intervint Descartes. J’aurais pu économiser beaucoup d’encre et de temps si j’avais connu ce système.

– Par ailleurs, poursuivis-je sur ma lancée, cette relation est antisymétrique. Si un concept en généralise un autre qui le généralise lui-même, alors ces deux concepts sont identiques. Disons, si tous les blups sont des blops et tous les blops sont des blups, alors blup et blop veulent dire la même chose.

– Sage décision, qui me paraît tomber sous le sens. Je la note donc :

∀(c,d) ∈ C², (c ≼ d) ∧ (d ≼ c) ⇒ c = d.

René, vous noterez ce petit chapeau ; il signifie « et ». La flèche, elle, signifie « implique que ».

– Enfin, la relation est transitive : si un concept en spécialise un autre qui spécialise un troisième, alors il spécialise aussi ce dernier.

– Parfait !

Et de noter une troisième équation :

∀(a,b,c) ∈ C³, (a ≼ b) ∧ (b ≼ c) ⇒ a ≼ c.

– Nous venons de définir ce qu’on appelle en maths une relation d’ordre partiel, et l’ensemble des concepts est un ensemble partiellement ordonné. C’est un exemple de structure mathématique abstraite : sans même savoir ce qu’est exactement un concept, nous pouvons raisonner dessus en utilisant tous les résultats qui ont été établis en mathématiques pour ce type d’ensemble. A titre d’exemple, sur la base de ce que nous savons, nous allons prouver l’existence de concepts dits minimaux. Considérez une chaîne de concepts tous différents, chacun spécialisant son voisin de droite. Nous pouvons partir d’un concept donné (il en existe au moins un puisque C n’est pas vide), et placer à sa gauche un autre concept qui le spécialise (si on en trouve un), par exemple :

[triangle rouge] ≼ [triangle]

Puis recommencer avec ce nouveau concept :

[panneau « céder le passage »] ≼ [triangle rouge] ≼ [triangle]

Et encore :

[panneau « céder le passage » à l’entrée du rond-point de Plouche-Les-Oyes] ≼ [panneau « céder le passage »] ≼ [triangle rouge] ≼ [triangle]

Nous continuons d’agrandir la chaîne par la gauche tant que c’est possible. Vous êtes d’accord que cette chaîne doit se terminer à un moment ?

– Oui, bien sûr. Nous avons décidé qu’il n’y avait qu’un nombre fini de concepts au total, donc cette chaîne elle-même doit être finie.

– Cela veut dire que nous avons placé à gauche un concept que rien ne spécialise sauf lui-même. Sinon nous aurions pu encore étendre la chaîne. Le concept tout à gauche est minimal. Vous voyez ? Nous avons prouvé l’existence de certains concepts particuliers uniquement en nous basant sur la structure de l’ensemble C, sans savoir vraiment ce qu’est un concept et sans nous en préoccuper. Du moment qu’un ensemble partiellement ordonné est fini et non vide, il contient des éléments minimaux, c’est tout. Nous pourrions tout aussi facilement démontrer qu’il existe des concepts qui n’ont pas d’autre généralisation qu’eux-mêmes, et que nous appellerons concepts maximaux.

– Voici un outil très puissant !

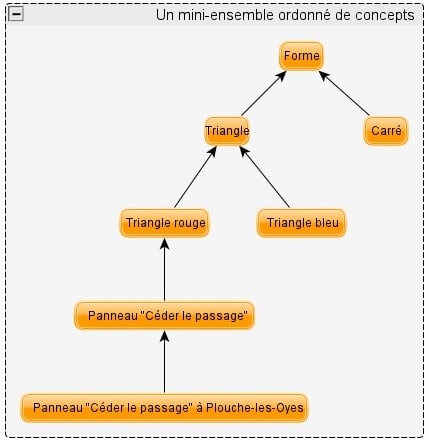
– D’une manière similaire, on peut montrer que si un concept n’est pas maximal, alors parmi tous les concepts plus généraux que lui, il en existe au moins un qui lui est adjacent, c’est-à-dire qui n’est séparé de lui par aucun autre concept. Par exemple, [triangle rouge] spécialise [triangle] qui lui-même spécialise [forme] ; bien que [forme] généralise [triangle rouge], il en est séparé par [triangle]. En revanche, aucun autre concept ne peut être inséré entre [triangle rouge] et [triangle], donc ces deux concepts sont adjacents. On peut représenter un ensemble fini partiellement ordonné en représentant deux éléments adjacents par des points reliés par des flèches, comme dans ce dessin:

– Merci, cela rend les choses plus concrètes.

– En effet. A présent, résumons rapidement ce que nous venons de faire, car vous allez bientôt vous réveiller. Nous avons formalisé quelques-unes de vos intuitions sur ce qui caractérise un concept pensable par une conscience autre que divine : il y en a un nombre fini non nul, et deux concepts peuvent être liés par la relation entre un concept particulier et un concept plus général. L’ensemble des concepts est ainsi partiellement ordonné. Nous en avons déduit qu’il contient nécessairement des concepts minimaux (qui n’ont pas d’autre spécialisation qu’eux-mêmes) et des concepts maximaux (qui n’ont d’autre généralisation qu’eux-mêmes). Nous n’avons fait qu’effleurer le sujet, mais c’est un début.

– Un très bon début ! Grand merci à vous. Pourrais-je vous revoir demain ?

– Avec plaisir, je n’ai rien de prévu. Passez donc à mon bureau de l’Ecole Normale. A demain, donc !

À suivre…