 Après quelques heures de sommeil profond et réparateur, nous nous retrouvâmes Corty et moi dans le bureau de Galois. Le caillou était en train de raconter à ce dernier son expérience dans la bouche de Démosthène.
Après quelques heures de sommeil profond et réparateur, nous nous retrouvâmes Corty et moi dans le bureau de Galois. Le caillou était en train de raconter à ce dernier son expérience dans la bouche de Démosthène.
– Nous voici de retour, déclarai-je. Qu’est-ce qu’on fait maintenant ?
– Je vous proposerais bien d’explorer un peu plus notre nouvelle définition de l’équivalence conceptuelle, écrivit Corty. Par exemple, voici un treillis symétrique; nous pourrions regarder quels concepts équivalents il contient.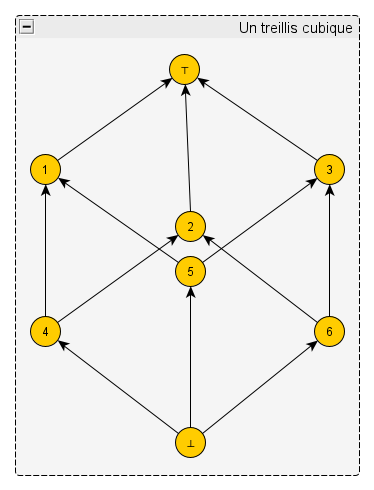
– C’est joli, intervint le caillou. Ce dessin ressemble à un cristal cubique, comme la pyrite.
– Très bien, dit Galois. Cher Corty, pourriez-vous dessiner ce que l’on obtient quand on supprime chaque concept du treillis d’origine ?
– Certainement. Voici ce que cela donne. Je me suis permis de réorganiser un peu les dessins en déplaçant certains concepts pour mieux faire apparaître les similarités :
 – Voilà qui est remarquable, commenta Galois. Nous voyons tout de suite que les trois dessins du haut se superposent, ainsi que les trois du milieu. Cela nous indique que les concepts 1,2 et 3 sont tous équivalents, ainsi que les concepts 4,5 et 6. Quant aux concepts minimum et maximum, ils restent chacun isolés dans leur classe.
– Voilà qui est remarquable, commenta Galois. Nous voyons tout de suite que les trois dessins du haut se superposent, ainsi que les trois du milieu. Cela nous indique que les concepts 1,2 et 3 sont tous équivalents, ainsi que les concepts 4,5 et 6. Quant aux concepts minimum et maximum, ils restent chacun isolés dans leur classe.
– Pourrions-nous dessiner le treillis que l’on obtient si on relie les classes par des flèches ? demandai-je.
– Oui, répondit Galois, mais il nous faut définir un ordre sur les classes d’équivalence, comme nous l’avions fait lors de notre dernière tentative. Notre relation d’équivalence conceptuelle a changé de définition, donc rien ne garantit que l’ordre que nous avions défini entre les classes fonctionne encore. Par exemple, ma démonstration d’antisymétrie ne marche plus, me semble-t-il.
– Si cela ne vous dérange pas, maître, intervint Corty, je propose de remettre les maths à plus tard. Je commence à fatiguer. De toute façon pour cet exemple là, au moins, je n’ai aucun mal à regrouper les concepts par classes en fusionnant les flèches au passage. Voyez :
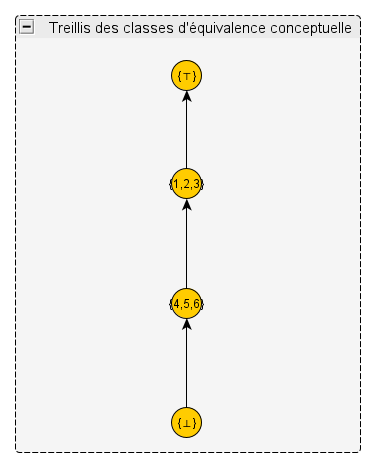 – Dites donc, s’exclama le caillou, ce treillis là contient aussi des concepts redondants, comme Animal et Chien dans votre exemple de tout à l’heure!
– Dites donc, s’exclama le caillou, ce treillis là contient aussi des concepts redondants, comme Animal et Chien dans votre exemple de tout à l’heure!
– Excellente remarque, dit Galois. En fait, quand on enlève n’importe lequel de ces quatre concepts, on obtient le même dessin aux noms près. Cela signifie qu’une fois les concepts regroupés en classes d’équivalence, le treillis résultant doit aussi être étudié. Quand on y découvre des concepts équivalents, il faut aussi les regrouper, et ainsi de suite
– Dans ce cas-ci, dis-je, on obtient une seule classe qui contient tout ! Un treillis avec un seul concept, qui est à la fois le minimum et le maximum ! Autant dire qu’il n’y a rien du tout, comme concept subjectif, dans ce treillis! Voyez vous-mêmes :

– C’est un peu troublant, dit Galois, mais est-ce si étonnant ? Notre treillis d’origine était hautement symétrique. Comment une subjectivité pourrait-elle se développer dans un monde où tout ressemblerait à tout ? Nous ne savons pas encore à quoi ressemble un treillis de concepts subjectifs, mais il doit être très dissymétrique. Nous cherchons un treillis dont chaque concept appartient à sa propre classe d’équivalence, ce n’est pas une condition si évidente.
– Pour ma part ça ne m’étonne aucunement, conclut le caillou. La pyrite est un minéral parfaitement stupide. J’aurais pu vous dire dès le départ qu’il ne peut y avoir aucun concept là-dedans.
(à suivre)









0 commentaires