Plus ou moins rasséréné, il m’a tout de même fallu quelques semaines pour digérer tout cela, laisser passer les fêtes, puis réfléchir enfin posément à ce que m’avait dit Abel.

D’abord, revenir aux fondamentaux. Que propose jusqu’ici notre théorie ? D’une part, les concepts subjectifs sont organisés en treillis fini. Deux concepts y ont une conjonction – un concept le plus général possible qui spécialise les deux – et une disjonction – un concept le plus spécifique qui généralise les deux. D’autre part, un concept subjectif n’est défini que par ses rapports aux autres concepts de ce treillis.

Fondamentalement, c’est tout. Par la suite, nous avions ajouté deux constatations empiriques et intuitives, dont je me demande si elles forment des axiomes ou sont conséquence de ce qui précède : un treillis de concepts ne comporte aucune symétrie ; un treillis de concepts ne comporte pas de concepts redondants.

Bien. Comment repartir de là, sans retomber dans le piège de l’interprétation dont m’a tiré Abel ?

Quelque chose me frappe d’un coup, que j’aurais dû voir bien plus tôt : si un concept subjectif n’est défini que par ses rapports avec les autres, cela implique que deux treillis de concepts subjectifs isomorphes sont nécessairement égaux.

Qu’est-ce que cela veut dire, et pourquoi est-ce important ? Je m’explique. Un treillis, c’est un ensemble d’objets structurés par une relation d’ordre partiel et qui assure que deux objets ont un « plus petit » objet « plus grand » qu’eux, et un « plus grand » objet « plus petit » qu’eux. Deux treillis sont isomorphes si je peux les dessiner de manière à ce que les dessins se superposent. En général, on peut très bien mettre ainsi en correspondance deux treillis différents, contenant des objets différents. Par exemple, je peux construire un treillis sur l’ensemble des nombres 1, 2, 3 et 6, où un nombre est « plus petit » qu‘autre s’il le divise. 1 est le plus petit élément de ce treillis, et divise tous les autres. 6 est le plus grand, divisé par tous les autres. 2 et 3 sont divisé par 1, divisent 6 et ne se divisent pas l’un l’autre. Je peux également, de manière indépendante, construire un treillis sur un ensemble de mots comme « mer », « merle », « amer » et « laminer », dans lequel un mot est « plus petit » qu’un autre si toutes ses lettres s’y trouvent. « mer » est l’élément minimum car ses lettres se retrouvent dans tous les autres mots ; « laminer » est l’élément maximum car il contient toutes les lettres de chaque autre mot ; « merle » et « amer » ne sont pas comparables.

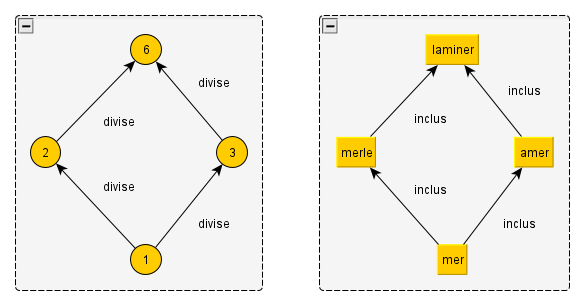
Ces deux treillis sont isomorphes, car je peux les dessiner de façon à ce qu’ils se superposent, en faisant correspondre le nombre 1 au mot « mer », 6 à « laminer » et (par exemple) 2 à « merle » et 3 à « amer ». Toutefois ce sont deux objets bien différents, l’un étant un ensemble de nombres et l’autre un ensemble de mots.

Le cas des concepts subjectifs est tout différent. D’après notre définition, un concept n’a aucune identité propre, hormis ses rapports avec les autres ; c’est un point sans caractéristique qui ne se distingue des autres que par sa place dans un dessin. De ce fait, un treillis de concepts subjectifs est entièrement décrit par son dessin et par rien d’autre. Si on peut superposer les dessins de deux treillis de concepts subjectifs, ils ont le même dessin et sont donc par définition identiques. Un treillis de concepts subjectifs n’est donc isomorphe qu’à lui-même.

Ce raisonnement s’applique également aux concepts individuels. Chacun des deux treillis que nous venons de construire présente une symétrie. Il est possible de dessiner le premier de deux manières différentes, en échangeant 2 et 3, et les deux dessins se recouvrent. 2 et 3 sont donc symétriques dans ce treillis. Cependant il s’agit bien de deux nombres différents que nous pouvons identifier sans ambigüité. De même, les mots « amer » et « merle » jouent un rôle symétrique dans le deuxième treillis, mais n’en restent pas moins de mots différents et parfaitement identifiés.

En revanche, un concept subjectif n’est qu’un point sans aucune caractéristique propre autre que sa place relative aux autres dans le dessin du treillis. En particulier, comme me l’a rappelé Abel, le nom par lequel nous désignons un concept n’est en rien une caractéristique ni une propriété de ce concept ; c’est juste un moyen commode de le désigner parmi les autres. Le nom Rien, par exemple, n’est qu’un raccourci commode pour désigner « le seul concept du treillis qui spécialise tous les autres ».

Si je peux dessiner un même treillis de concepts subjectifs de deux manières différentes qui se superposent en déplaçant des concepts, les deux dessins obtenus sont alors indiscernables ; il n’y en de fait qu’un seul, et il n’existe aucun moyen d’y distinguer deux concepts ainsi superposés. De tels concepts sont donc par définition identiques. En d’autres termes, de par sa définition même, un treillis de concepts subjectifs ne peut pas contenir de symétrie (en termes mathématiques, on dirait qu’il ne présente aucun autre automorphisme que l’identité).

Bien, une bonne chose de réglée. Maintenant, revenons à cette histoire de rapports entre concepts. Ce que ma définition implique, c’est qu’une fois connus les rapports entre concepts, je dois être capable de reconstituer le treillis correspondant et la place qu’y occupe chaque concept, sans aucune ambigüité.

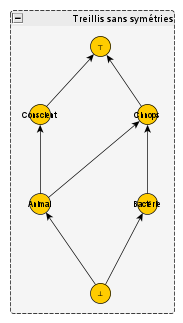
Très bien, mais il faut formaliser plus précisément, pour un concept donné, ce que sont ses « rapports avec les autres concepts de ce treillis ». C’est flou, essayons de clarifier cela. Je reprends pour exemple notre fameux treillis supposé sans symétries ni redondances, celui qui a soulevé l’ire du caillou :

Il existe de multiples manières de décrire les relations d’un élément de treillis avec d’autres. Je pourrais, par exemple, me contenter de donner, pour chaque concept, la liste de ses successeurs – ou tout simplement, je pourrais décrire chaque flèche du treillis en spécifiant son origine et son extrémité. C’est d’ailleurs une manière classique en informatique de décrire ce genre de structure. Mais cette technique fonctionne avec tout ensemble ordonné, or nous travaillons spécifiquement avec des treillis, et même avec une classe particulière de treillis. Il serait logique d’en tenir compte.

Un treillis offre deux moyens immédiats de calculer des « rapports » entre deux concepts a et b : je peux calculer leur conjonction (a ⋏ b) et leur disjonction (a ⋎ b).  Je pourrais ainsi construire la liste exhaustive des conjonctions et disjonctions de concepts dans mon treillis. Comme les deux opérations ⋎ et ⋏ sont commutatives (a ⋏ b = b ⋏ a ) et idempotentes (a ⋏ a = a ), je peux me restreindre aux cas ou les deux concepts sont différents et pris dans un ordre déterminé. Je devrai alors spécifier deux identités pour chaque paire de concepts, ce qui en fait tout de même 30 pour notre exemple.

Je remarque cependant que beaucoup de ces calculs sont redondants. Par exemple, si je sais que Animal ⋎ Bactérie = Chnops, je peux et je dois en déduire que Animal ⋎ Chnops = Chnops et que Animal ⋏ Chnops = Animal, car la disjonction de deux concepts généralise chacun d’eux ; or la disjonction d’un concept c avec un concept qui le généralise est ce dernier, et leur conjonction est c lui-même. De telles égalités « dérivées » n’apportent aucune information supplémentaire ; je devrais donc pouvoir m’en passer.

Par ailleurs, je remarque que quand nous définissons un concept, nous ne le comparons jamais à un seul autre concept ; nous le considérons toujours en fonction d’au moins deux autres concepts différents. Nous ne disons pas « un animal est un chnops » mais « un animal est un chnops conscient », ce dont nous pouvons également conclure qu’un animal est un chnops si besoin. De même nous ne disons pas « les chnops comprennent les animaux » mais plutôt « les chnops comprennent les animaux et les bactéries ». Dans tous ces exemples, je manipule au moins trois concepts différents.

J’ai du coup bien envie de proposer la règle qui suit : Un concept est défini par les expressions du type a = b ⋏ c ou a = b ⋎ c dans lesquelles il apparaît (dans le rôle de a, b ou c), et où les trois concepts sont différents.

Trouver ces expressions à partir d’un treillis fini quelconque n’a rien de difficile : il me suffit de calculer la conjonction et la disjonction de tous les couples d’éléments qui ne sont pas comparables entre eux (l’un ne généralise ni ne spécialise l’autre). J’obtiens pour chaque paire une ligne (a, b, a ⋏ b, a ⋎ b) où tous les éléments sont différents.

Revenons à notre exemple. Je calcule la conjonction et la disjonction de tous les couples de concepts incomparables entre eux. Il n’y en a que trois :

A	B	a ⋏ b	a ⋎ b
Animal	Bactérie	Rien	Chnops
Chnops	Conscient	Animal	Quelque chose
Conscient	Bactérie	Rien	Quelque chose

 

Ce tableau est un condensé de l’information disponible dans mon treillis, que je pourrais résumer ainsi : les animaux et les bactéries sont des chnops ; un animal est un chnops conscient ; les bactéries et les êtres conscients n’ont rien en commun. Et c’est tout.

Si j’en crois ma définition d’un treillis de concepts subjectifs, je devrais être capable de reconstituer mon exemple à partir de ces égalités, sans aucune ambigüité. Je vais donc chercher le treillis le plus simple possible où je peux attribuer un nom comme Rien ou Chnops à chaque élément, de manière à ce que les égalités ci-dessus soient respectées. Puisque mes concepts ne sont définis que par ces égalités, je devrais trouver une solution unique.

Remarquons immédiatement que le treillis « trivial », qui ne contient qu’un seul élément, satisfait toutes ces conditions. Si j’attribue tous les noms à cet unique élément, alors bien sûr Animal, Bactérie et Rien désignent le même élément, qui est sa propre conjonction et sa propre disjonction avec lui-même. Cette solution nihiliste, bien entendu, ne me satisfait pas. Implicitement, je souhaite attribuer des noms différents à des concepts différents. Mais qu’est-ce qui me garantit, dans le tableau ci-dessus, que deux noms différents doivent effectivement désigner des éléments différents du treillis ?

Je dispose d’une information supplémentaire : par définition même de ces égalités, les quatre noms qui apparaissent dans chaque ligne de mon tableau sont censés désigner des concepts différents, car ils désignent deux concepts non comparables ainsi que leur conjonction et leur disjonction. Je cherche donc un treillis dans lequel Animal, Bactérie, Rien et Chnops désignent des éléments deux à deux différents, soit un treillis qui contient au moins quatre éléments. Je sais également que tous ces éléments sont généralisés par Chnops ; or la deuxième ligne du tableau m’indique que Chnops est différent de Quelque chose et le spécialise. Je peux en déduire que Animal, Bactérie, Rien, Chnops et Quelque chose sont deux à deux différents ; le treillis que je cherche doit avoir au moins cinq éléments.

Le nom Conscient, qui manque dans cette liste, pourrait-il désigner l’un d’entre eux ? Eh bien non : la deuxième ligne me dit que Conscient est différent de Chnops, Animal et Quelque chose ; la troisième ajoute que Conscient est différent de Bactérie et de Rien. Le nom Conscient doit donc désigner un sixième élément distinct de tous les autres. Je cherche un treillis à 6 éléments – mais pas plus car je cherche le treillis le plus petit respectant les égalités du tableau.

Essayons maintenant de reconstruire ce treillis. Je considère d’abord la première ligne du tableau :

a	B	a ⋏ b	a ⋎ b
Animal	Bactérie	Rien	Chnops

 

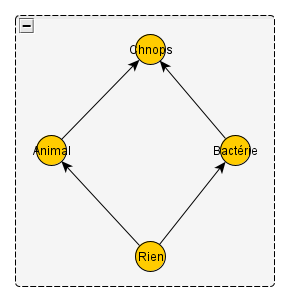
Quel est le plus petit treillis qui satisfasse ces conditions ? Facile. Il n’y en a qu’un, et c’est celui-ci :

Je sais que ce treillis ne comporte que quatre éléments, que Animal et Bactérie n’y sont pas comparables, mais qu’ils sont tous les deux plus généraux que Rien et plus spécifiques que Quelque chose. Bon, j’ai assigné arbitrairement le nom Animal à l’élément de gauche, alors que j’aurais pu le mettre à droite ; mais les autres relations devraient me permettre de le distinguer de Bactérie et de rendre cette solution unique.

Effectivement, si l’on regarde maintenant la deuxième ligne :

a	B	a ⋏ b	a ⋎ b
Chnops	Conscient	Animal	Quelque chose

 

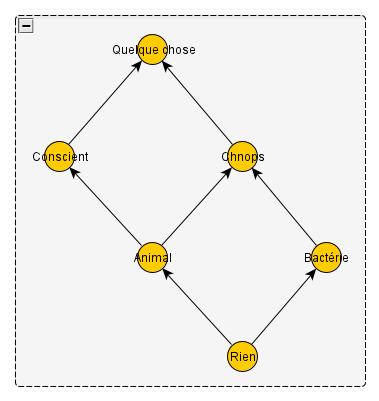
Elle introduit deux nouveaux concepts, Conscient et Quelque chose, qu’il me faut placer. Je vois que Conscient généralise Animal, qu’il est incomparable avec Chnops, et qu’il spécialise Quelque Chose – lequel généralise également Chnops. Je peux même être sûr que Conscient est incomparable avec Bactérie, car sinon Chnops comme Conscient généraliseraient à la fois Animal et Bactérie, et ces derniers auraient deux disjonctions, ce qui est interdit dans un treillis. J’obtiens donc ceci :

Enfin, considérons la troisième ligne :

a	B	a ⋏ b	a ⋎ b
Conscient	Bactérie	Rien	Quelque chose

 

Elle n’introduit aucun nouveau concept, mais me permet de confirmer que le treillis cherché est bien celui que j’ai déjà et que mes définitions sont cohérentes.

Ca parait très bien, mais j’ai peut-être simplement eu de la chance ? Est-ce qu’un seul treillis répond vraiment à mes définitions ? Je vous passerai les détails qui sont pénibles, mais la réponse est oui.  En traitant les lignes dans l’ordre inverse, par exemple, je retrouve le même treillis – cette fois-ci en insérant des concepts entre deux concepts déjà placés. Par ailleurs, si j’énumère tous les treillis possibles à 6 éléments, je constate qu’un seul satisfait les égalités demandées.

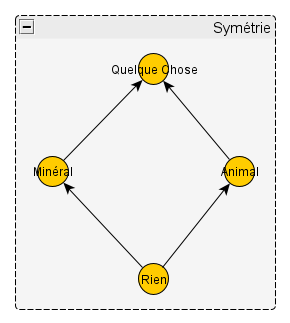
Parfait ! Ma proposition identifie donc bien mon exemple fétiche comme un treillis de concepts subjectifs. J’ai pu reconstruire ce treillis à partir de sa définition, après avoir prouvé que tous les concepts y sont distincts, et y associer un nom à chaque élément sans ambigüité possible. Qu’en est-il maintenant des contre-exemples ? Considérons d’abord un treillis symétrique. Je considère l’exemple le plus simple possible :

En explicitant les relations entre concepts non comparables, je n’obtiens qu’une ligne :

a	b	a ⋏ b	a ⋎ b
Animal	Minéral	Rien	Quelque chose

 

Je peux évidemment reconstruire un treillis en utilisant cette information. Les quatre concepts sont distincts, il me faut donc un treillis à quatre éléments. Deux de ces éléments sont incomparables ; ils généralisent tous deux le troisième et spécialisent le quatrième. Facile. En revanche, quel nom assigner à quel élément du treillis obtenu ? Je peux assigner sans ambigüité le nom Rien à l’élément minimum et Quelque chose à l’élément maximum ; en revanche je peux nommer Animal celui de gauche ou celui de droite, à ma guise, car rien ne les distingue, et aucune autre inégalité ne peut les différencier. Le nom Animal peut donc être assigné à deux éléments différents du treillis. Or deux concepts différents devraient toujours être discernables à partir de leurs définitions ; je devrais toujours pouvoir associer à chacun un nom sans ambigüité. Mon exemple n’est donc pas un treillis de concepts subjectifs, ce que nous avions déjà établi.

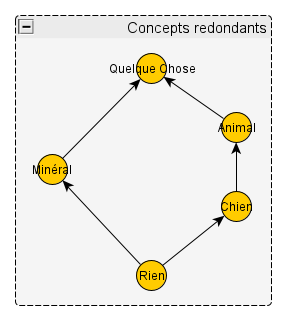
Se pose enfin la question des concepts redondants, comme Chien et Animal dans l’exemple proposé par Galois. Nous ne voulons pas de tels concepts ; notre définition permet-elle également de les éliminer ?  Je vais encore partir d’un exemple le plus simple possible :

Les relations entre concepts non comparables sont dans ce tableau :

a ⋏ b	a	b	a ⋎ b
Rien	Animal	Minéral	Quelque chose
Rien	Chien	Minéral	Quelque chose

 

Puis-je reconstruire le treillis à partir de ces définitions ? Eh bien, j’arrive facilement à ceci :

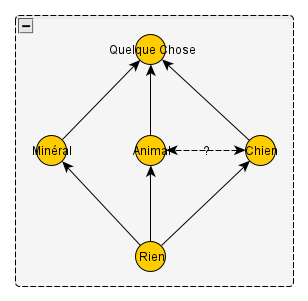
En effet je sais que Minéral, Animal, Rien et Quelque chose sont tous différents ; de même Chien est différent de Minéral, Rien et Quelque chose. Tous les éléments spécialisent Quelque chose et généralisent Rien, que je peux donc placer. Je peux établir que les deux concepts Chien et Animal sont comparables, sinon on me donnerait leur conjonction et leur disjonction ; Minéral, par ailleurs, peut être distingué des deux car il n’est comparable ni avec l’un ni avec l’autre. Mais au-delà, je suis coincé. Rien dans le tableau ci-dessus ne me permet de savoir lequel des deux concepts Animal et Chien généralise l’autre. De plus et surtout, rien dans ce tableau ne me permet même d’établir que ces deux concepts sont différents. De fait, si je fusionne les deux éléments Chien et Animal, j’obtiens un treillis à quatre éléments dans lequel les noms Animal et Chien désignent le même élément : ce treillis satisfait lui aussi les deux égalités du tableau et garde bien distinct les concepts qui doivent l’être. Ce treillis plus simple est différent de mon exemple, lequel n’est donc pas non plus un treillis de concepts subjectifs.

Je crois que je tiens là quelque chose de solide. Un treillis de concepts subjectifs peut être reconstitué à partir de ses relations entre éléments non comparables, comme étant le plus petit treillis qui satisfait ces relations. Sa définition garantit que les quatre concepts de chaque ligne sont deux à deux distincts, et assigne un seul nom à un seul élément du treillis. La définition d’un treillis contenant des symétries permet en revanche d’associer un même nom à plusieurs éléments, et ne convient pas. Celle d’un treillis contenant des redondances permet, à l’inverse, d’associer plusieurs noms à un même élément, et ne convient pas non plus. C’est assez élégant somme toute, et sans aucune « interprétation » malvenue.

Bon, ben faut s’y remettre. Merci Abel. Galois, Corty, et euh.. Œil de taureau, vous êtes où ?

(à suivre)