La dernière livraison du Coin des traîtres – dont je suis fan – s’intéresse à la traduction des nombres (on en apprend de belles !) et pose en conclusion la question du rapport entre la traduction et les maths. On pourrait la trouver saugrenue tant ces deux domaines paraissent aux antipodes l’un de l’autre – comment les maths dans leur glaçante pureté pourraient-elles rendre compte de ce qui est avant tout un art du compromis amoureux, soumis à des contraintes aussi ineffables qu’essentielles, ancré dans le réel, et arbitré autant par le parcours humain de la traductrice que par ses connaissances linguistiques ? Or il s’agit là, bien au contraire, d’une question des plus fécondes.

Si l’on s’intéresse à la traduction des maths, il semble pourtant y avoir bien peu à en dire ; les maths, dans les faits, ne comportent guère de nombres et, quand même ils en parlent, ne leur donnent que leur pauvre signification bêtement arithmétique. Aussi la belle variété linguistique du nombre, sa couleur, son parfum de terroir y sont-ils en général totalement perdus, au point de rendre le problème de traduction d’un ennui mortel. Voici une version simplifiée en anglais du premier théorème fondamental de l’analyse (résultat passionnant par ailleurs et auquel nous pourrions revenir) :

En voici une traduction française :

On ne peut pas dire que l’exercice soit passionnant. Certes, il faut savoir que Analyse (l’étude des fonctions) se dit Calculus en Anglais ; l’on pourra noter la différence de notation pour un intervalle ouvert (un ensemble de nombre qui contient tous les nombres entre ses extrémités mais pas ces dernières) ; les conventions typographique sont quelque peu différentes. Mais c’est à peu près tout… quant au grand théorème de Fermat :

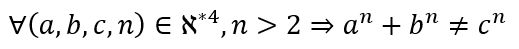
il peut être compris tel quel par n’importe quel mathématicien sur cette planète (même si ce n’est pas le cas de sa démonstration par Andrew Wiles, un monstre de plus de cent pages !). La mathématique serait-elle donc la langue d’avant Babel ? Peut-être mais, dans ce cas, de quoi nous parle-t-elle si ce n’est d’elle-même ? Comme le relève Francis Wolf dans son excellent ouvrage Pourquoi la musique ? [1], de nombreux auteurs considèrent la musique comme un langage qui est son propre signifié. En est-il autrement des maths ? Et cette réflexivité est-elle liée à l’universalité perçue de l’une comme de l’autre ? En serait-elle une condition nécessaire ? C’est peut-être cela, la complexité de la traduction : le prix à payer pour l’utilisation d’une langue qui ne parle pas que d’elle-même, mais bien du réel.

Il existe pourtant une branche des maths qui, justement, se spécialise dans l’étude des structures et du raisonnement mathématiques, et que l’on appelle métamathématique. L’un de ses résultats les plus populaires est le théorème d’incomplétude de Gödel, dont nous avons déjà parlé. Or, la métamathématique, en mélangeant la forme au fond, soulève de fort intéressants problèmes de traduction. En effet, l’objet étudié par la métamathématique est l’énoncé mathématique lui-même. Sa forme, sa structure y deviennent sujets d’étude. D’abstrait et conceptuel, l’énoncé devient alors charnel, concret, réel, lié au langage qui le porte. Un énoncé métamathématique parle d’autres énoncés, établis à l’aide de règles lexicales et grammaticales arbitraires mais bien définies, et pourquoi pas en langage pseudo-humain. Il peut spécifier, par exemple, que la phrase deux plus trois égale quatre est à la fois grammaticalement correcte et sémantiquement fausse, ou que cette même phrase comporte cinq mots.

Tous les textes qui vulgarisent le théorème de Gödel [2] abondent d’exemple de tels énoncés, donnés en langage naturel pour familiariser les lecteurs à cette forme de raisonnement. Parmi eux, il en est de fascinants : ce sont ce que l’on appelle des énoncés autoréférentiels, qui parlent d’eux-mêmes. Parmi les exemples les plus connus : Cette phrase pas de verbe ; cette phrase est grammaticalement correcte si l’on ne tient pas compte de sa dernière lettres ; et le savoureux cette phrase contiens exactement trois ereurs (je vous laisse les trouver). De fait, l’énoncé autoréférentiel peut presque revendiquer sa place en tant que sous-genre littéraire (de niche, tout de même !), et il soulève en tout cas des problèmes de traduction bien à lui.

Comment traduiriez-vous en français les phrases qui suivent :

Since this sentence has been written in english, its translation to french is a lie.

Had this sentence been written in french, it would not start with a verb.

This sentence contains exactly fifty-four printable symbols.

Un petit défi pour Christilla Vasserot et ses complices du Coin des traîtres !

Yannick Cras

[1] Francis Wolf, Pourquoi la musique ?, Fayard, 2015.

[2] Il en est de bons et d’exécrables. Je ne peux que recommander l’excellent ouvrage de Douglas Hofstadter, Gödel, Escher, Bach : les brins d’une guirlande éternelle (Interéditions, 1985 / Dunod, 2008), un livre culte chez les geeks et auquel j’emprunte certains de mes exemples. Hofstadter est également l’auteur d’un livre magnifique, Le Ton beau de Marot (en Français dans le texte), consacré entre autres à la traduction du français vers l’anglais, et qui présente la particularité, pour cette raison même, d’être proprement intraduisible en français !

Yannick Cras
Le nombre imaginaire

GuardarGuardarGuardarGuardarGuardarGuardarGuardarGuardarGuardarGuardar

GuardarGuardar