Alors que je finissais de retranscrire mon rêve de la nuit précédente, régulièrement interrompu par l’œil de taureau qui s’était réveillé très excité et voulait tout savoir, Corty me fit remarquer un oubli :

– Nous avons complètement omis de parler à Galois de cette autre observation de Sima, au sujet de notre petit treillis de concepts subjectifs, celui avec qui nous jouons depuis des semaines et dont Galois voudrait connaître le sens. Je vais l’appeler le Mini-Treillis, puisqu’apparemment c’est le plus petit treillis de concepts subjectifs possible. Sima nous a signalé le fait que quand on tourne son dessin d’un demi-tour, on obtient le même dessin au sens des flèches près. Vous vous en souvenez ? Nous devrions y réfléchir.

Je relus cette remarque tout haut pour le bénéfice du caillou avant de répondre :

– Tu as raison. D’autant que la plupart des treillis que nous avons considérés jusqu’ici semblent partager cette propriété, qui n’est pourtant pas universelle. Le Songe d’Everett, par exemple, présente lui aussi cette symétrie verticale.

– Je me suis souvenu d’un article que nous avons lu il y a quelques temps, qui en parlait. Il s’agit de ce qu’on appelle un treillis autodual.

– Mais oui ! C’est vrai !

– Et si vous m’expliquiez ? intervint le caillou.

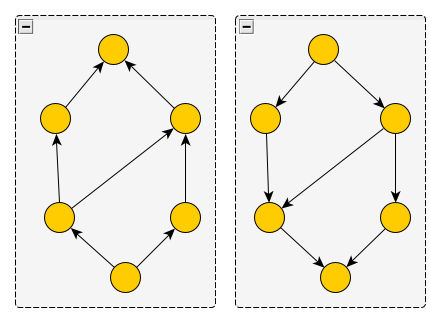
– Eh bien, considère un treillis, avec ses deux opérations de conjonction et de disjonction. Tu peux construire un autre treillis en utilisant les mêmes éléments et en échangeant les deux opérations ; la conjonction de deux éléments dans le nouveau treillis, c’est leur disjonction dans le treillis initial, et vice-versa. Ce nouveau treillis est appelé treillis dual du premier. L’ordre y est aussi inversé :  si un élément est plus petit qu’un autre dans le treillis initial, il se retrouve plus grand que lui dans le treillis dual. L’élément minimal du premier treillis (que nous supposerons fini, comme d’habitude) devient l’élément maximal du treillis dual, et vice-versa.  Et tu obtiens un dessin du treillis dual en retournant le treillis initial et en inversant le sens de flèches. Par exemple :

– Je vois, dit le caillou. Si je comprends bien, alors, le dual du dual, c’est le treillis de départ ? Ce serait logique de retomber sur lui, si je tourne encore le dessin de 180° et que j’inverse une fois de plus les flèches.

– Mais oui, tout-à-fait, le félicitai-je. Chaque treillis est le dual de l’autre.

– Et dans le cas qui nous intéresse, continua Corty, il se passe quelque chose de particulier : le treillis est isomorphe à son dual, et leurs dessins se recouvrent.  C’est ce que l’on peut appeler un treillis autodual. Chaque élément du treillis peut ainsi se superposer avec un élément du treillis dual, que l’on peut appeler son élément dual. Le dual du dual d’un élément, bien sûr, c’est cet élément lui-même. Reste à savoir si c’est important pour nous, ou si nous sommes tombés par hasard sur ce type de treillis.

– Le mieux, ce serait de regarder comment ça se passe pour Le Songe d’Everett, puisque nous connaissons déjà la signification de chaque élément.

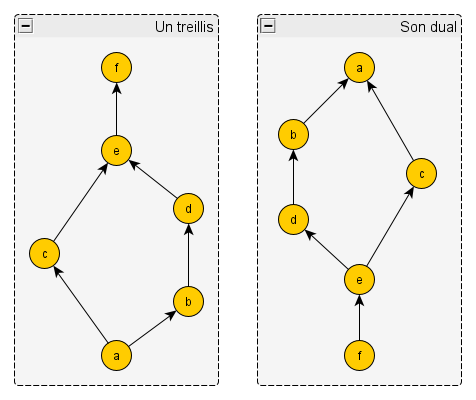
– Bonne idée. Notons que, comme ce treillis est très symétrique, il y aurait différentes manières de le superposer avec son dual ; mais il y en a une qui me paraît vraiment naturelle, et c’est celle-ci :

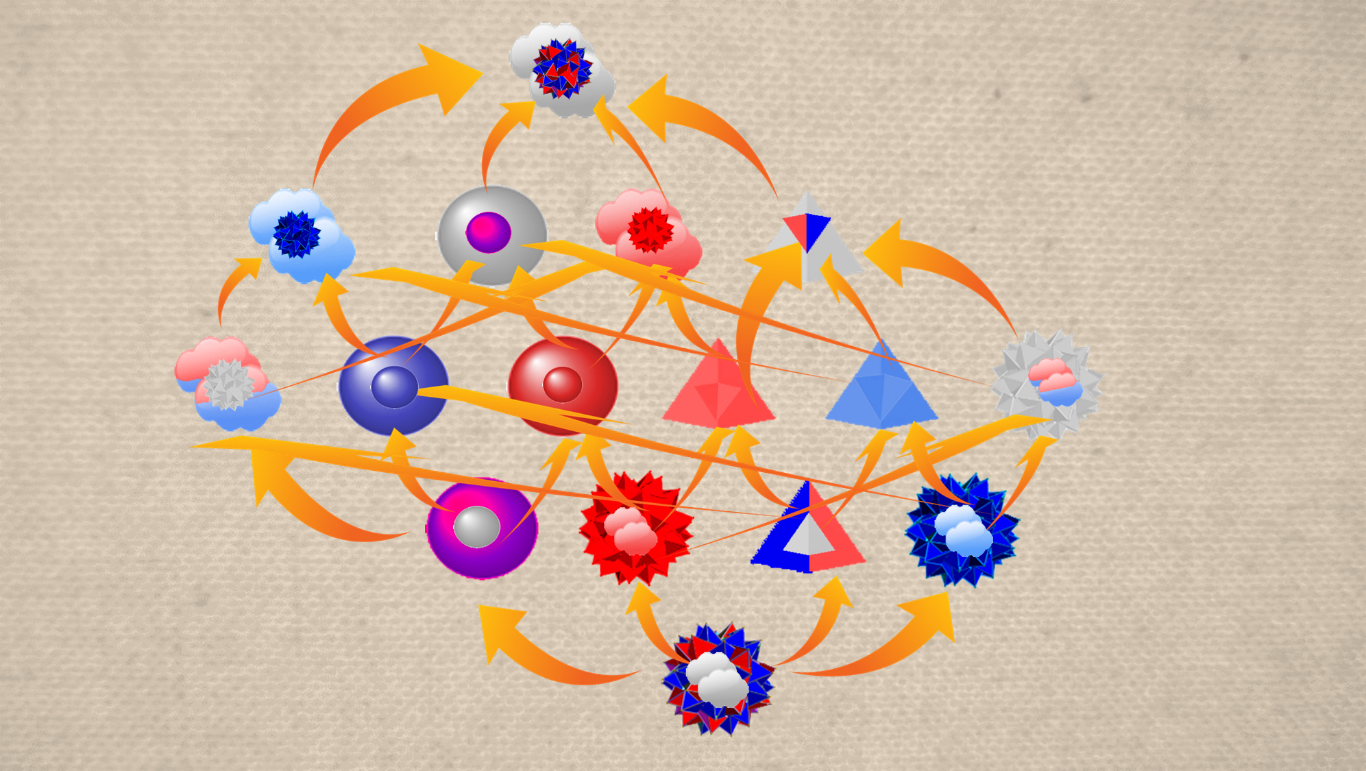
Vous voyez, j’ai retourné le treillis de 180°, j’en ai un peu réarrangé les éléments, et j’ai inséré le dual de chaque élément à l’intérieur, en plus petit. En revanche je n’ai pas représenté les flèches inversées, pour garder le dessin lisible. Mais si vous inversez les flèches mentalement, vous verrez que ça marche : on retrouve le treillis inversé.

– Pourquoi as-tu modifié l’ordre des éléments du treillis dual ? Si tu t’étais contenté de tourner le treillis de 180°, ça marchait aussi.

– Oui, mais du coup le dual du cercle bleu, par exemple, aurait été le triangle bleu. Or je trouve ça très arbitraire. Pourquoi le triangle bleu plutôt que, disons, le cercle rouge ? D’ailleurs si Sima avait choisi une représentation différente de son treillis, c’est ce qu’on obtiendrait. Puisqu’on a le choix, je trouve plus logique de décider que chaque objet, chaque forme colorée concrète, est son propre dual. En fait, maintenant que j’y pense, il y a une autre justification possible.

– Laquelle ? voulut savoir le caillou.

– Eh bien, Galois nous a expliqué que le treillis de Sima est un produit de deux petits treillis, vous vous souvenez ? Or chacun de ces petits treillis est lui-même autodual. Par exemple :

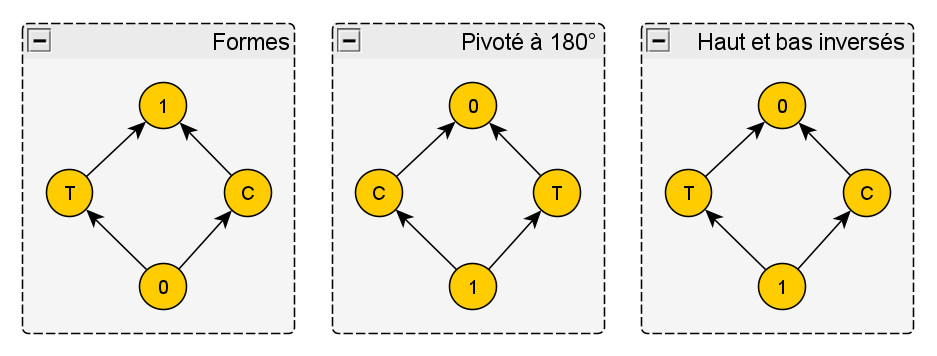
Je peux superposer ce treillis à son treillis dual de deux façons : soit en le faisant pivoter de 180°, soit en inversant le haut et le bas comme dans un miroir. Le dual de 0 est toujours 1 et vice-versa ; mais dans un cas le dual de T est C (et vice-versa), alors que dans l’autre le dual de T est lui-même, et idem pour C.  Dans le premier cas, je fais correspondre chaque élément à son « contraire », en quelque sorte. Quelque chose c’est le contraire de rien, et Triangle est le contraire de Cercle. C’est une notion connue, en algèbre on appelle ça un complémentaire. Mais dans notre cas, je trouve plus intuitif d’adopter l’autre transformation, celle qui échange 0 et 1 et qui associe T et C à eux-mêmes. Pour fixer les idées, je vais noter a* le dual d’un élément a. Je peux donc écrire : 0* = 1 ; 1* = 0 ; T* = T ; C* = C.

– D’accord, dit le caillou. Jusqu’ici ça me va.

– Ensuite, je fais la même chose pour l’autre petit treillis, celui des couleurs. Là, je remarque que le treillis produit de deux treillis autoduaux est lui-même autodual, et je peux trouver une définition naturelle du dual d’un élément de ce produit. Comme vous vous en souvenez, chaque élément du produit est un couple (f, c) constitué d’un élément f du treillis des formes et d’un élément c du treillis des couleurs. Eh bien, je décrète que le dual de ce couple est le couple qui contient le dual de f et celui de c. En d’autres termes : (f, c)* = (f*, c*).

– Et tu obtiens la correspondance que tu nous as montrée, conclus-je. C’est malin.

– C’est intéressant, dit le caillou. On dirait que chaque concept qui… disons évoque… un ensemble d’objets (attention, je ne dis plus que c’est un ensemble !) a pour dual le concept qui évoque les propriétés communes à ces objets. Ce que je veux dire, c’est que Objet triangulaire a pour dual Forme triangle, or la seule propriété que les objets triangulaires ont en commun, c’est justement la forme triangle. Le dual de Quelque chose, c’est Rien, et vice-versa ; or si je considère l’ensemble de tous les objets, il n’y a aucune propriété commune à tous, et l’ensemble vide a toutes les propriétés. Si j’osais, je dirais que chaque extension est le dual d’une intention, et vice-versa.

On nous l’a changé, le caillou. Finies, les remarques sarcastiques. J’ai l’impression qu’il a été échaudé par sa dernière et catastrophique intervention ; il a vraiment envie que ça marche.

– Très juste, releva Corty, tout aussi étonné que moi. Quant aux objets concrets, comme le triangle rouge, on peut dire que le même concept représente à la fois l’unique objet Triangle rouge – donc une extension, même limitée à un seul élément – et l’ensemble de ses propriétés : Forme triangle, Couleur rouge – donc une intention. Il est du coup logique que chaque objet soit son propre dual.

– Reste le cas des éléments Forme et Couleur, qui sont chacun le dual de l’autre, notai-je. C’est un peu étrange. Il est vrai cependant que le concept Forme a comme propriétés de présenter toutes les couleurs en même temps, et aucune forme imposée, ce qui correspond bien à ce qu’exprime le concept Couleur. Chacun de ces concepts représente les propriétés de l’autre.

– En tout cas, dit Corty, le dual d’un élément du treillis s’obtient toujours en inversant les 0 et les 1 dans le couple de valeurs qui le définit. Le calcul est facile. Mais n’oublions pas que le treillis que nous considérons n’est pas un treillis de concepts subjectifs, accessible à une conscience, mais plutôt de concepts « objectifs », qui décrivent exhaustivement le mini-monde considéré. La question, maintenant, c’est de savoir si un treillis de concepts subjectifs devrait, lui aussi, être auto-dual.

– J’ai une petite idée là-dessus, proposa le caillou d’une voix timide. Je peux essayer ?

Sous-entendu : Je ne risque pas de tout foutre en l’air une fois de plus ?

– Mais je t’en prie !

– Eh bien, si je comprends bien, nous envisageons que les concepts subjectifs d’une conscience pourraient être obtenus à partir d’un treillis de concepts « objectifs » qui décrit le monde, symétrique et régulier comme le Songe d’Everett – en beaucoup plus grand et compliqué, bien sûr ?

– C’est l’idée, confirma Corty.

– Mais il faudrait extraire un treillis très asymétrique de cet immense treillis symétrique, pour que des concepts subjectifs intéressants y apparaissent. Il faudrait « oublier » beaucoup de concepts du treillis d’origine, et n’en conserver que certains pour que, dans ce nouveau treillis, ils soient discernables les uns des autres.

– Absolument, l’encourageai-je. Le Songe d’Everett, tel qu’il est, ne porte aucun concept subjectif intéressant, parce qu’il est tellement symétrique qu’il n’y a aucun moyen de faire la différence entre un triangle et un cercle ou entre le rouge et le bleu.

– Alors arrêtez-moi si je dis une bêtise, mais il me semble aussi que les concepts sélectionnés par une conscience devraient avant tout provenir de ses perceptions, des situations concrètes qu’elle rencontre, de l’état réel du monde à un moment donné. Les autres concepts seraient des abstractions, sous forme d’ensembles ou de propriétés communes, de ces situations concrètes. Par exemple, le concept de « forme triangulaire » n’aura d’intérêt et de sens que si la conscience rencontre des triangles concrets, et même des triangles de couleurs différentes. Ce sont les seules perceptions qu’elle peut avoir.

– Intéressant, dit Corty. Continue.

– Donc, imaginons qu’une conscience perçoive le monde comme une succession de formes colorées. Pour introduire une asymétrie, supposons qu’il n’existe aucun triangle bleu dans son expérience. La conscience choisira dans le Songe d’Everett les concepts qu’elle perçoit directement (cercles rouges ou bleu, triangle rouge), et les concepts qui sont reliés à ceux-là, mais pas les autres.

Cela m’évoquait quelque chose :

– Un concept qu’on perçoit directement comme part de l’expérience…. Ce n’est pas ce qu’on appelle un percept en philosophie ?

– Tu as raison, répondit Corty. Les philosophes opposent les percepts et les concepts, mais nous avons choisi pour notre part de les unifier ; tu te souviens de notre discussion sur la pensée en tant que perception et la prise de conscience nécessaire de ce que l’on perçoit. Quoi qu’il en soit, le caillou a clairement raison : notre expérience sensible du monde est avant tout une histoire de percepts. Le concept plus abstrait arrive après. Tu ne peux pas percevoir l’ensemble des cercles ; tu ne peux percevoir à chaque instant qu’un vrai cercle concret, bleu ou rouge. Bien sûr, ce que moi je perçois en tant que cortex visuel est bien différent, mais le premier concept qui te viendra à l’esprit à toi, ce sera un objet concret avec une forme et une couleur, que nous pouvons appeler un percept pour ce qui te concerne.

– Eh bien, reprit le caillou, ces concepts particuliers, concrets, ces percepts donc, ils semblent jouer un rôle, comment dire, de pivot dans le treillis que tu as représenté. J’ai l’impression que chaque concept se comporte symétriquement par rapport à son dual vis-à-vis de ces percepts. Par exemple, le concept Objet triangulaire est la disjonction de Triangle rouge et Triangle bleu dans le Songe d’Everett ; or leur conjonction, c’est justement son dual Forme triangle.

– Oui, dit Corty, c’est dû au fait qu’un percept est son propre dual. De ce fait, la conjonction de deux percepts est le dual de leur disjonction. Les deux opérations se comportent de manière symétrique vis-à-vis des percepts.

– Donc, conclut le caillou, quelle que soit la manière dont une conscience choisit des concepts possibles reliés aux percepts qu’elle perçoit, je trouverais logique qu’elle choisisse toujours un concept et son dual, ou alors aucun des deux, puisque les deux jouent des rôles symétriques par rapport à ces fameux percepts.

Oh, mais c’est diablement intéressant, cela, me dis-je in petto.

Corty eut la même pensée :

– C’est une riche idée, bravo. Regardez, je dessine le treillis qu’on peut extraire du Songe d’Everett en supposant qu’il n’y a jamais de triangles bleus. C’est ce qu’on appelle le sous-treillis engendré par l’ensemble des autres percepts. On obtient ceci :

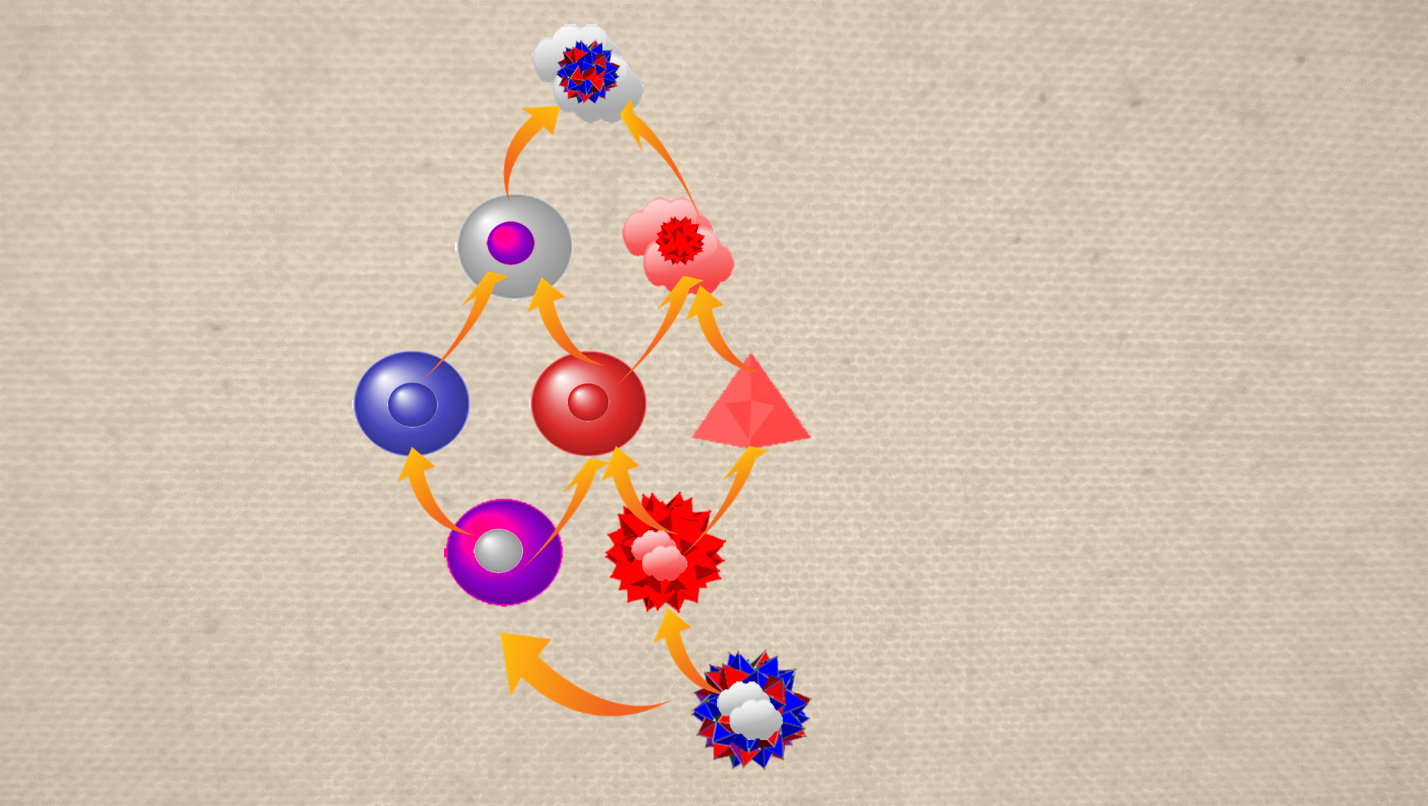
– Beaucoup de concepts ont disparu, s’étonna le caillou. Il n’y a même plus de concept de forme ou de couleur !

– C’est logique, au fond. Dans un monde tel que celui-là, le seul objet bleu est toujours un cercle, donc la notion d’objet bleu et celle de couleur bleue se confondent avec Cercle bleu. De même, il n’y a plus de notion de triangle (objet triangulaire ou forme triangle) puisque tout ça se condense en Triangle rouge. On a toujours le concept d’objet circulaire et son dual, la forme cercle, parce qu’il existe des cercles des deux couleurs ; et on a toujours un concept d’objet rouge avec son dual la couleur rouge, parce qu’il existe plusieurs objets rouges. Mais comme il n’y a plus qu’un seul concept de forme, la forme triangle, on n’a pas besoin d’un concept plus général de forme. De même, comme la seule couleur identifiée comme telle est le rouge, il n’y a pas besoin d’un concept de couleur.

– Bien sûr, repris-je, ce qu’on obtient n’est pas réellement un treillis de concepts subjectifs, parce que le cercle bleu est encore symétrique avec le triangle rouge, et que l’on pourrait les confondre. Mais, en supposant qu’on puisse les garder différenciés en utilisant d’autres propriétés non représentées ici, c’est intéressant. On voit que les concepts qui restent vont par paire, chacun avec son dual, comme prévu. Ce treillis est encore autodual. Bravo, Œil de taureau. Belle intuition de ta part.

– Merci. Est-ce que nous sommes en train de dire, avança le caillou, qu’un treillis de concepts subjectifs devrait toujours être autodual, en plus de ses autres propriétés ?

– Intuitivement, ça me paraît assez convaincant, approuvai-je. Si je peux penser à un groupe d’objets, je peux aussi penser aux propriétés qu’ils ont en commun. Ce sont deux concepts très proches, mais pas identiques, sauf dans le cas d’un percept où les deux se confondent.

– Je suis également de cet avis, mais avec un petit bémol. Nous avons de bonnes raisons de penser que si les percepts jouent un rôle central dans la construction des concepts subjectifs d’une conscience, alors le treillis de concepts subjectifs est toujours autodual. Mais je vous ferai remarquer que le cas du Mini-Treillis est différent : ce treillis est certes autodual, mais il ne contient aucun percept !

– Que veux-tu-dire ? m’étonnai-je. Comment peut-on même parler de percept dans ce cas ?

­– Eh bien, nous avons avancé que les percepts jouent un rôle pivot dans la construction des concepts de plus haut niveau d’une conscience, et garantissent l’autodualité du treillis subjectif, uniquement parce qu’un tel concept est son propre dual. Dans notre exemple du Songe d’Everett, les concepts qui ont cette propriété sont bien les concepts « concrets », des formes précises avec des couleurs précises, les percepts donc. C’est ce qui a donné au caillou sa bonne idée. Mais dans le cas plus général des concepts subjectifs, nous ne savons pas de quoi sont faits les concepts, n’est-ce pas ? Nous ne pouvons considérer que leurs relations entre eux, pas leur anatomie individuelle que nous ne sommes pas supposés connaître. C’est pour cela, d’ailleurs, que Sima a représenté tous les éléments du Mini-Treillis de manière identique, sans même leurs donner de nom individuel.

– D’accord, dit le caillou. Et donc ?

– Et donc, dans un treillis comme celui-là, nous ne pouvons plus parler d’objet concret ou non, de forme, de couleur, ou quoi que ce soit du genre. En revanche, nous pouvons tout de même définir une notion de percept. Il nous suffit de décréter arbitrairement qu’un concept s’appelle un percept s’il est son propre dual. C’est une définition parfaitement précise, d’autant plus que dans un treillis de concepts subjectifs, il n’y a aucune symétrie ; si un tel treillis est autodual, il n’y a qu’une seule manière de trouver le dual d’un élément donné.

– Très bien, dis-je, cela nous donne une idée plus générale de ce que peut être un percept parmi les autres concepts, sans égard à un cas particulier. Je vote pour.

– Et, poursuivit Corty, une fois cela fait, nous pourrions même réintroduire une notion d’ensemble ou plutôt d’extension, et une notion de propriété ou d’intention. Il nous suffit de décréter qu’un concept plus général qu’un percept est une extension, et qu’un concept moins général qu’un percept est une intention. Il est facile de montrer que deux percepts ne sont jamais comparables, et que les seuls concepts qui sont à la fois des intentions et des extensions sont les percepts eux-mêmes. Il nous reste à considérer les concepts qui ne sont pas leur propre dual et qui ne sont comparables avec aucun percept, comme c’est le cas avec Forme et Couleur dans le Songe d’Everett. Ceux-là, je propose de les appeler des attributs. Nous conservons ainsi, dans un treillis de concepts subjectifs, toutes les propriétés qui nous ont plu dans le Songe d’Everett. Par exemple, la disjonction de deux percepts est une extension – quelque chose qui évoque un ensemble – et leur conjonction est une intention qui est le dual de cette extension – quelque chose comme une propriété partagée par les éléments d’un ensemble. Et la conjonction d’un percept avec un attribut est une intention, tout comme la conjonction de l’attribut Couleur et du percept Triangle Rouge est la propriété Couleur Rouge dans le Songe d’Everett.

Tiens, je vous dessine un petit exemple :

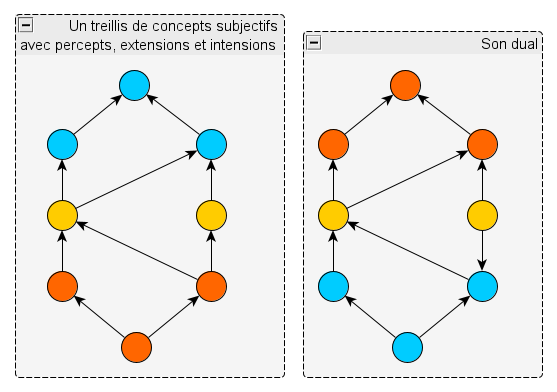
Sauf erreur de ma part, ce treillis n’a ni symétrie ni concepts redondants ; de plus il est autodual. Pour obtenir le dual, il suffit d’inverser le haut et le bas en miroir. Les deux concepts en orange sont des percepts (chacun est son propre dual) ; les concepts en bleu sont des extensions, et ceux en rouge les intentions. Il n’y a pas d’attribut, car ici tous les concepts généralisent ou spécialisent des percepts.

J’observe d’ailleurs que l’on peut extraire un treillis avec la exactement même forme du Songe d’Everett sans triangle bleu. En voici un :

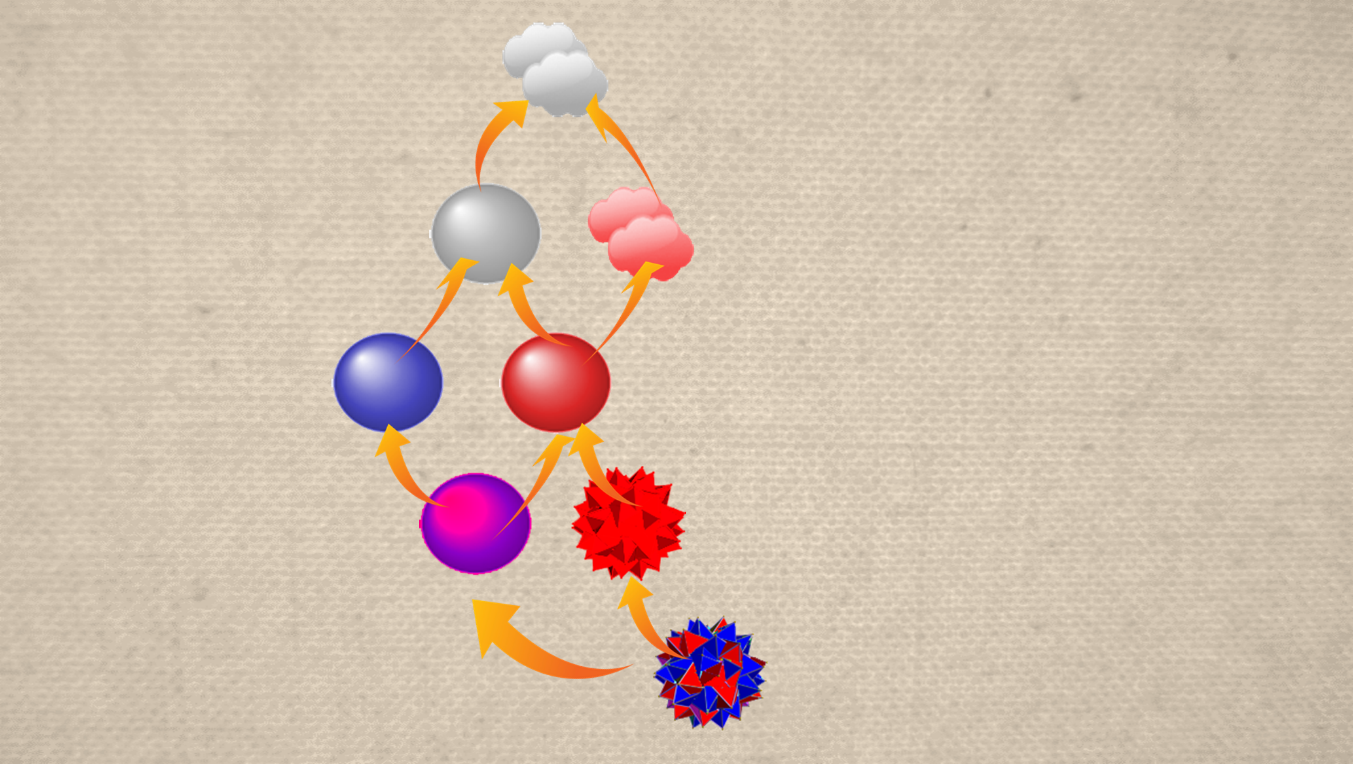
En percevant un cercle de chaque couleur, nous pouvons évoquer le concept de cercle (extension ou intention). Si en plus nous imposons l’existence de la couleur rouge (en intention ou en extension), nous obtenons ce treillis. En revanche la couleur bleue n’existe pas en tant que telle dans ce monde. Et les « attributs » Forme et Couleur non plus.

– Mmmm… Comment pourrait-on imposer l’existence de la couleur rouge en tant que concept différent du cercle rouge, si c’est le seul objet rouge ?

– Je ne sais pas, avoua Corty, mais peut-être parce que les triangles rouges seraient très rares dans ce monde, et qu’une conscience aurait oublié leur existence pour une raison quelconque ?  Il resterait juste une forme d’asymétrie entre les cercles bleu et rouge, suffisante pour ne pas confondre les deux concepts.

– En tout cas j’adore ! dit le caillou. Vos définitions nous permettent de raisonner sur les concepts subjectifs en nous abstrayant totalement de la nature physique des objets que nous manipulons, et en même temps de nous en rapprocher quand nous le désirons !

– Oui, félicitations ! ajoutais-je.

– Merci, répondit peu modestement Corty ; je dois dire que je suis assez fier de cette idée. Cependant, voilà mon petit bémol : dans le Mini-Treillis, qui est tout de même à l’origine de notre discussion, aucun concept n’est son propre dual. Il suffit de regarder le dessin que j’ai reproduit au début. Chaque concept en recouvre un autre, différent, dans le treillis dual. Il n’y a donc aucun percept là-dedans – et pas d’intention ni d’extension non plus.

Nous en restâmes bouche bée (figurativement dans le cas du caillou).

– Le plus bizarre, c’est que je peux tout de même extraire le Mini-Treillis de notre univers sans triangle bleu ; j’ai même compté six manières de le faire. En voici deux pour l’exemple :

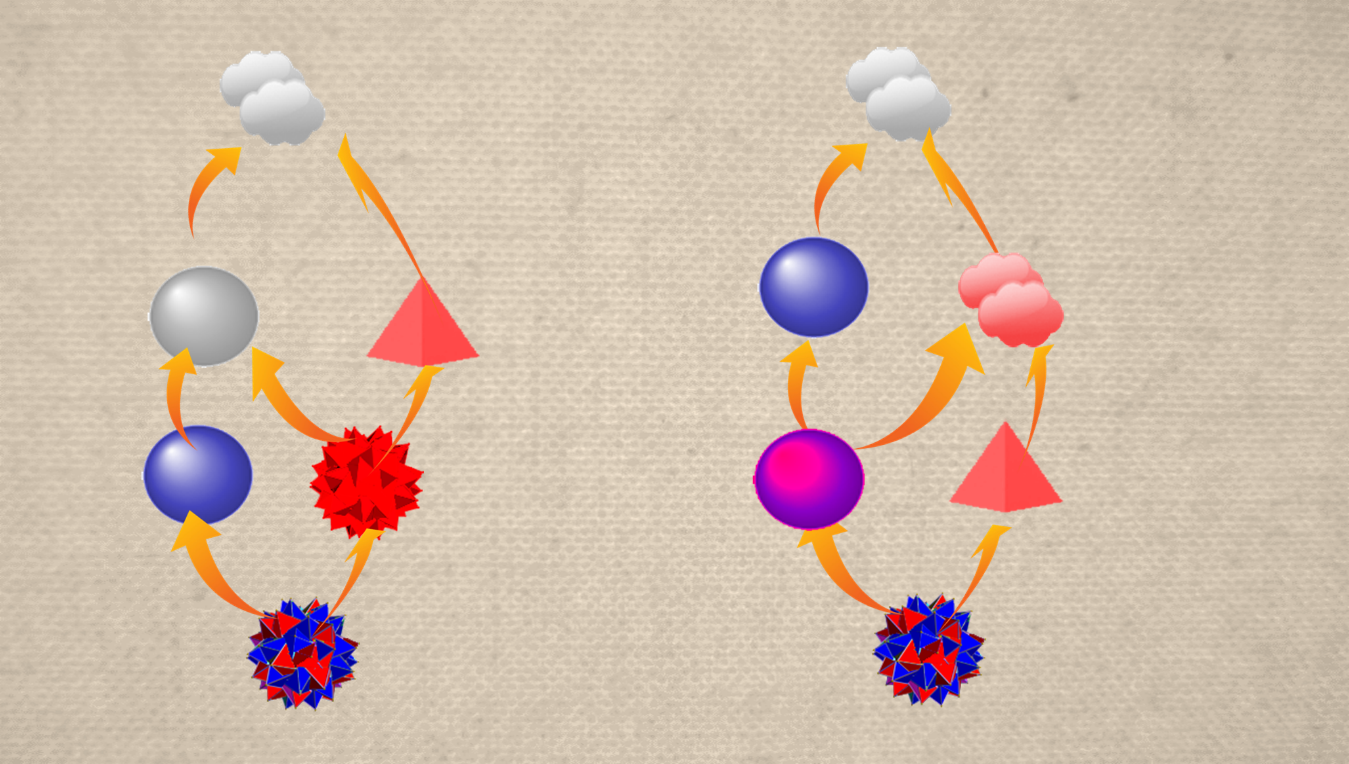
Vous voyez, pour reproduire le Mini-Treillis, je suis obligé de casser la symétrie qui nous paraît si naturelle : certains concepts du Songe d’Everett apparaissent sans leur dual. Par exemple, à gauche, en voyant un cercle bleu et un triangle rouge, je pense à un objet circulaire mais pas à la forme cercle ; je pense à la couleur rouge mais pas aux objets rouges. A droite c’est l’inverse. C’est vraiment bizarre. Et dans ces deux treillis, si je les retourne, aucun concept n’est son propre dual. On se retrouve avec des recouvrements assez curieux, par exemple les objets circulaires et la couleur rouge. Et puis, pourquoi une conscience choisirait-elle un de ces treillis plutôt qu’un autre ? Je ne sais pas comment interpréter tout ça, mais ça n’a plus grand-chose à voir avec notre intuition de la manière dont nous percevons le monde, en tout cas.

– Cela voudrait-il dire, hésita le caillou, qu’il pourrait y avoir des consciences sans perception ? sans quoi que ce soit qui en joue le rôle ?

– Je ne sais pas, murmurai-je. Et franchement, je ne suis pas sûr d’avoir envie de le savoir.

(à suivre)