À l’origine du conflit qui incita Tex Avery à quitter la Warner pour la Metro-Goldwyn-Mayer se trouve la loi de la chute libre. À la fin de The Heckling Hare (1941), Bugs Bunny et le chien Willoughby tombent deux fois de suite d’une falaise vertigineuse. Sur fond de hurlements horribles, la chute est terrifiante, d’autant que l’on ne sait trop ce qu’il advient de Bugs et de son copain. Le producteur Leon Schlesinger oblige Avery à modifier la séquence : une chute suffira, et les personnages devront freiner juste avant l’arrivée au sol. Avery est furieux et proteste. Le Hollywood Reporter du 2 avril 1941 titre : “Cartoon man walks out on Leon Schlesinger !” (Un “cartoonist” affronte Schlesinger). À la suite de quoi Avery, viré de la Warner, est aussitôt engagé par MGM. Voici la version censurée :

Dans cette séquence, la loi de la chute libre est globalement respectée, sauf à la fin et au début : Bugs, qui tombe après Willoughby, le rattrape, ce qui est interdit par les lois de la physique puisque tous les corps tombent à la même vitesse. Jules Verne lui-même l’avait bien compris : dans De la Terre à la Lune, le chien éjecté hors de l’obus lunaire suit fidèlement ce dernier. En somme, Schlesinger et Avery ont tous les deux une mauvaise note à leur cartoon de physique.

Le freinage (par antigravité ?) avant l’atterrissage est devenu un grand classique du dessin animé. La façon de tomber en est un autre : il arrive souvent chez Avery que lorsqu’on coupe un arbre (Timber !!), il tombe du mauvais côté en dépit des lois de la pesanteur. Surtout, comme chez le vil coyote de Chuck Jones, il n’est pas rare de voir un personnage courir, et continuer sur sa lancée en dépassant le bord de la falaise. Il finit par s’arrêter, se gratte la tête et réalise qu’il est dans le vide, ce qui déclenche sa chute immédiate — à la verticale. Or cette “théorie du coyote suspendu” est loin d’être absurde, comme va le montrer un petit détour par l’histoire des sciences.

C’est Galilée, au début du XVIIe siècle, qui a débrouillé le problème : un coyote emporté par son élan et dépassant le bord d’une falaise tombe en décrivant une parabole, comme on peut le voir en donnant une pichenette à une bille posée sur une table, et s’écrase au sol d’autant plus loin qu’il court vite. Cette chute parabolique peut être décomposée en deux mouvements : l’un, horizontal, à vitesse constante, jusqu’à la verticale du point d’impact, et l’autre, vertical et accéléré, pour rejoindre le sol. Le coyote suspendu est donc une décomposition parfaitement légitime du mouvement de chute libre. Cette variante trouvée chez Chuck Jones, disciple d’Avery, décompose encore plus le mouvement, et est donc encore plus drôle :

Dans la scène classique, le pouvoir comique tient à la durée du temps de réflexion du coyote… qui en a fait réfléchir beaucoup. Un certain S. R. Gould (sans doute un pseudonyme) a fait paraître en 1993 dans la revue New Scientist un article intitulé “Loony Tuniverse” où il propose une intéressante alternative : si l’on admet que la gravité est une forme d’énergie comme une autre, rien ne s’oppose à ce que l’énergie propre du coyote équilibre celle de la gravité, le coyote étant alors en lévitation. Mais si le coyote se met à penser en réalisant qu’il est au-dessus du vide, il utilise une certaine énergie (mentale), créant un déséquilibre qui se traduit par sa chute.

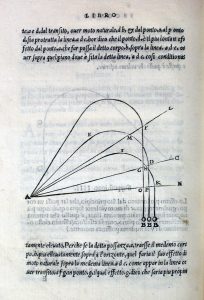L’énergie mentale étant difficile à définir, force est d’en rester à la décomposition du mouvement. Comme le regard télescopique, la théorie du coyote suspendu a donc une longue histoire. On trouve chez Tartaglia (1606), juste avant que Galilée ne la démonte, une théorie analogue : ses boulets de canon, au lieu de décrire une honnête parabole bien symétrique, montent tout droit, font un petit cercle (le temps de se demander ce qu’ils vont faire ensuite), puis tombent à la verticale ! Et l’on trouve la même erreur, plus ou moins accentuée, chez les peintres du XVIIe siècle représentant des jets d’eau. Le rire du cartoon, une fois de plus, flirte étroitement avec l’histoire des idées.

Nicolas Witkowski
Chroniques avéryennes

[print_link]