Le lendemain soir, je retrouvai un Evariste à l’œil pétillant, sourire béat aux lèvres, affalé sur le petit sofa qui ornait un coin de son bureau. Son rendez-vous s’était visiblement bien passé. Il m’accueillit d’ailleurs en bondissant de joie :

– Ravi de vous revoir, mon cher ! Je ne sais pourquoi nos conversations me mettent toujours de si joyeuse humeur.

Nos conversations, vraiment ? Ou ce petit mot d’une écriture fine sur papier parfumé que je vois trainer sur son bureau ? Quoi qu’il en soit :

– J’en suis ravi, maître. Je suis impatient de reprendre avec vous l’exploration du treillis de Galois.

– Avec plaisir. Je me suis d’ailleurs permis d’adopter pour cela un nouvel exemple simplissime, que j’espère plus facile à explorer.

Il me montra son tableau noir :

– Comme vous le remarquerez, j’ai opté pour un univers purement visuel, dans lequel nous considérons des formes colorées. Je pense que cela rendra les concepts plus faciles à visualiser. Par ailleurs, je n’ai pas donné de nom aux formes individuelles, afin de ne pas introduire d’ambiguïté quant à ce qui est une propriété et ce qui n’en est pas : ici, chaque forme n’est définie que par ses propriétés. Vous remarquerez d’ailleurs que toutes les formes ont des propriétés bien distinctes. J’ai simplement numéroté les lignes pour pouvoir les repérer dans l’extension de chaque concept.

– Je comprends. Cependant vous n’avez pas distingué les réponses « Oui » et « Non » pour chaque question, comme nous l’avions fait hier ?

– C’est vrai, mais elles sont implicites. Vous remarquerez que chaque ligne a une croix dans l’une des colonnes « Bleu » ou « Rouge » et pas dans l’autre ; de même elle a une croix dans exactement l’une des colonnes « Triangle » ou « Cercle ». De ce fait, tout ce qui est bleu est également « pas rouge » et vice-versa ; les deux propriétés « bleu » et « pas rouge » sont exactement équivalentes. De même pour « triangle » et « pas un cercle ». Si j’avais gardé les réponses « oui » et « non » pour chaque colonne, le treillis de Galois regrouperait dans un seul concept le fait d’être bleu et celui d’être « pas rouge », car il ne pourrait pas les distinguer. En fusionnant moi-même ces propriétés, comme indiqué dans les intitulés des colonnes, j’ai simplement gagné du temps et de la place.

– Puis-je essayer de dessiner le treillis de Galois associé à vos données ?

– Faites donc, je vous en prie.

Je dessinai ceci :

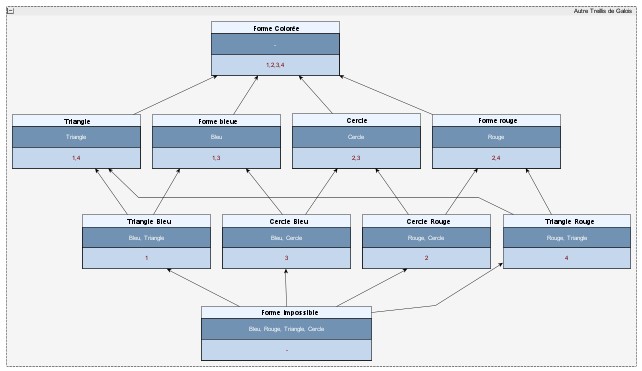
– Voici un beau dessin, très symétrique ! me félicita Galois.

– Merci ! Il me donne par ailleurs une idée. Puisque le concept de « forme rouge », par exemple, correspond comme vous me l’avez expliqué à un concept de « forme non bleue », j’imagine qu’on pourrait plus généralement définir le complément, la négation de chaque concept, le concept de ce qui n’est pas lui.  Nous pourrions même définir une nouvelle opération sur les concepts, qui associe à chaque concept sa négation !

– Hmmm… De tels treillis existent effectivement. On peut y définir une opération de « complément », par laquelle on associe à tout concept c un concept, noté c* par exemple, tel que c ⋏ c* = ⊥ et c ⋎ c* = ⊤. Dans notre exemple, nous constatons que la conjonction de [Forme rouge] et [Forme bleue] est [Forme impossible], qui est notre concept minimal ; c’est logique car rien ne peut être à la fois rouge et bleu. De même, la disjonction de [Forme rouge] et [Forme bleue] est [Forme colorée], notre concept maximal. Par ailleurs, chacun des quatre concepts correspondant à une forme concrète spécialise l’un ou l’autre de ces concepts. Cela traduit bien le fait que toute forme est rouge ou bleue. Cependant cela ne marche pas pour tous les concepts. Par exemple, nous n’avons ici aucun concept qui représente la négation de « triangle rouge », au sens où vous l’entendez.

– Ah bon ? Pourtant, un cercle bleu n’est ni triangle ni rouge ! D’ailleurs, si je regarde le dessin, la conjonction de [Cercle bleu] et de [Triangle rouge] est bien [Forme impossible], et leur disjonction – le concept le plus spécifique qui les généralise tous deux – est bien [Forme colorée] !

– C’est vrai, ces deux concepts sont complémentaires au sens où je viens de le définir, mais l’un n’est pas pour autant la négation de l’autre. Que faites-vous du concept [Triangle bleu] ? Il ne spécialise pas [Triangle rouge], mais il ne spécialise pas non plus [Cercle bleu]. Un triangle bleu n’est pas un triangle rouge, mais ce n’est pas non plus un cercle bleu. De même, un cercle rouge n’est ni un cercle bleu ni un triangle rouge. Or, ce que vous attendriez intuitivement de la négation du concept [Triangle rouge], c’est qu’elle généralise les trois formes qui ne sont pas des triangles rouges, et seulement celles-là. Aucun concept ne le fait ici.

– Je comprends. Mais c’est très dommage ! Cela veut dire que notre treillis de Galois n’est pas assez puissant pour représenter tous les concepts possibles ; car je peux bien penser, moi, au concept de ce qui n’est pas un triangle rouge !

– Je ne serai pas aussi pessimiste que vous. De fait, je ne pense pas que le treillis des concepts subjectifs d’une conscience possède une telle opération. Pas vraiment.

– Je ne comprends pas bien.

– Je m’explique. Tout d’abord, pouvez-vous visualiser le concept de forme rouge ?

– Bien sûr, c’est immédiat. Je vois un fond rouge, sans forme.

– Maintenant, visualisez le concept opposé de forme non rouge.

– C’est facile aussi ; je visualise un fond bleu.

– Parfait. Maintenant, visualisez un triangle rouge.

– Facile…

– et enfin, visualisez le concept de ce qui n’est pas un triangle rouge.

– Eh bien, euh, je vois un cercle bleu…

– Attendez ! Je ne vous ai pas demandé de penser à un exemple précis ; je vous ai demandé de penser au concept général « pas un triangle rouge ». Pouvez-vous le visualiser ?

– Euh… en fait pas vraiment. Je peux voir un triangle bleu ou un cercle quelconque, mais pas les deux en même temps. Et si je pense à un fond bleu, je ne peux pas en même temps penser à un cercle rouge.

– Exactement ! Votre conception de ce qui n’est pas un triangle rouge n’est pas facile à voir en esprit, alors que vous n’avez aucun problème avec les autres concepts que je vous ai demandé de visualiser. Intellectuellement, bien entendu, vous savez ce qu’est une forme qui n’est pas un triangle rouge ; mais il s’agit d’un concept beaucoup plus élaboré que celui de triangle rouge. D’ailleurs, il met bien plus de temps à s’installer dans l’esprit humain. Montrez les quatre formes de notre exemple à un jeune enfant, et demandez-lui ce qu’est le contraire d’un triangle rouge. Que répondra-t-il à votre avis ?

– Un cercle bleu, très certainement.

– Eh oui ! Beaucoup d’adultes auront la même réponse, d’ailleurs. Il n’y a guère que les mathématiciens pour répondre autre chose ; et pour cela ils s’appuient sur des outils bien plus abstraits que la visualisation. Vous n’avez pas en tête de créer la conscience d’un mathématicien, j’imagine ?

– Euh, non. Je cherche à imaginer une conscience aussi petite que possible, en fait.

– Eh bien voilà : si une conscience aussi élaborée que celle d’un jeune enfant ne peut pas visualiser d’instinct la négation d’un concept, c’est peut-être que ce mécanisme n’est pas essentiel à son fonctionnement.

– Et pourtant j’ai pu visualiser sans problème le concept de forme non rouge…

– Voilà. C’est seulement dans le cas où vous avez le choix uniquement entre deux propriétés complémentaires – rouge ou bleu, cercle ou triangle – que vous pouvez visualiser la négation d’un concept. Dès que vous avez plus de choix ou plus de combinaisons, cela devient impossible. En résumé, il paraît possible qu’à bas niveau, la notion de négation ne soit pas indispensable à la conscience.

– La bonne nouvelle, si je vous suis, c’est que les treillis de Galois ne sont donc pas disqualifiés. Mais il est un peu humiliant de penser que nous ne pensons pas « naturellement » quelque chose d’aussi élémentaire que la négation.

– Dans ce cas, préparez-vous à être encore plus humilié. Il y a autre chose que nous faisons très mal, c’est conceptualiser une collection de concepts disparates.

– Je ne comprends pas. Nous avons bien défini la disjonction de deux concepts ! Dans notre exemple, étant donnés deux concepts, nous pouvons toujours en trouver un qui les généralise tous les deux.

– Bien sûr, mais de manière très grossière, si je puis dire. Par exemple, la disjonction de [Triangle rouge] et de [Cercle bleu], c’est le concept de forme colorée tout entier. Pourtant, je suis sûr que vous pouvez penser à un concept plus fin ?

– Eh bien, on peut penser au concept de tout ce qui est soit un triangle rouge soit un cercle bleu. Il généralise bien les deux, et il est plus spécifique que le concept de forme colorée.

– Oui, mais trouvez-vous cela naturel ? Donneriez-vous un nom à une catégorie qui regroupe les triangles rouges et les cercles bleus, s’il n’y a aucune autre propriété en jeu ?

– Pas vraiment, non.

– Et d’ailleurs, dans votre vie quotidienne, pouvez-vous penser à des concepts que vous manipulez et dont les exemples n’ont aucun rapport entre eux ?

– Il y a bien l’inventaire de Prévert… Mais, sérieusement, non.

– Voilà. Nous sommes bien armés pour trouver naturellement des concepts qui représentent des propriétés communes à certains objets, ou des exemples communs à certaines propriétés, mais pas des ensembles arbitraires d’exemples. Nous donnons le nom « objet rouge » à tout ce qui est majoritairement rouge ; nous donnons le nom « famille » à un ensemble de personnes qui ont en commun de nombreuses propriétés. Mais nous n’avons pas de nom simple pour représenter une collection contenant les chiens, les symphonies, les enclumes et rien d’autre. Pour la même raison nous ne conceptualisons pas l’ensemble des objets qui ne sont pas des panneaux « laisser le passage ». Il s’agit dans les deux cas d’une collection bien trop diverse et hétéroclite.

– Pourquoi est-ce ainsi, à votre avis ?

– Je ne sais pas. C’est une excellente question, mais quelqu’un de plus versé que moi en psychologie et en physiologie humaine serait plus à même que moi d’y répondre. Reste en tout cas que les treillis que nous étudions semblent reproduire ces limitations, ce qui est plutôt bon signe.

– Vous pensez donc que le treillis de Galois est notre réponse ? L’ensemble de nos concepts subjectifs est un treillis de Galois extrêmement complexe construit à partir de propriétés binaires de type « oui/non », et le problème est résolu ?

–  Je n’ai pas dit cela. De fait, j’ai des doutes, que je n’arrive malheureusement pas à expliciter. Nous poursuivons certainement une piste intéressante, mais quelque chose me dit qu’actuellement nous avons en un sens trop de concepts, et que par ailleurs il nous en manque…

Galois s’interrompit à cet instant, les yeux écarquillés. Je pensai un instant qu’il réfléchissait mais m’aperçus que son regard était fixé vers son tableau que j’avais quitté des yeux, et vers lequel je me retournai.

A la place des dessins dont nous avions couvert le tableau, s’y présentait une note manuscrite à la craie blanche, en lettres cursives impeccables :

Médusé, Galois se tourna vers moi :

– Voudriez-vous, cher ami, avoir la bonté de m’expliquer ce qui se passe ?

(à suivre)