“Le Nombre imaginaire” ou les mathématiques comme terrain de jeu où l’imagination seule fixe les limites.
« Un bon schéma vaut mieux qu’un long discours ». Afin d’appréhender d’un coup d’œil l’essence des phénomènes parfois complexes qu’ils étudient, les scientifiques – géomètres puis physiciens en tête, mais aussi biologistes et économistes – ont toujours veillé à appliquer cet adage en en cherchant des représentations les plus parlantes et intuitives possibles. La géométrie fourmille ainsi depuis l’antiquité de démonstrations purement visuelles du théorème de Pythagore, qui se passent littéralement de mots, et que les techniques modernes rendent encore plus frappantes – telles que celle-ci.
René Descartes eut l’idée de relier l’algèbre à la géométrie, en introduisant ce que l’on appelle encore un repère cartésien et des coordonnées cartésiennes : on peut ainsi représenter tout point du plan par un couple de nombres, son abscisse – sa distance horizontale à un point d’origine donné – et son ordonnée – sa distance verticale à l’origine. On peut de cette manière associer à toute figure géométrique une ou plusieurs formules algébriques qui expriment une relation entre les abscisses et les ordonnées de chacun de ses points, et vice-versa. Ainsi, tous les points du cercle centré à l’origine et de rayon 1 vérifient la formule X2+Y2 = 1 ; à l’inverse, on peut associer un point à chaque couple de valeurs X et Y telles que Y = X2 + 2X + 1, ce qui donne une courbe appelée parabole (celle de nos récepteurs satellites). On peut dès lors, par exemple, étudier l’intersection de deux courbes en cherchant des couples de nombres X et Y qui satisfont simultanément leurs formules respectives et, à l’inverse, représenter géométriquement et intuitivement les solutions d’équations complexes.
Cette idée qui peut nous paraître anodine aujourd’hui représentait une révolution conceptuelle à l’époque, car elle rapprochait deux domaines de la pensée mathématique – la géométrie et l’algèbre – jusqu’alors totalement séparés. La géométrie algébrique est encore aujourd’hui un des champs les plus féconds de la pensée mathématique.
Le système de coordonnées dont nous parlons est très intuitif, et s’étend facilement à notre espace familier à 3 dimensions ; mais on peut utiliser des systèmes de coordonnées bien différents. Le mouvement d’une masselotte fixée à l‘extrémité d’un ressort peut, par exemple, être représenté comme une courbe dans un espace où la coordonnée horizontale – l’abscisse – représente le temps, et l’ordonnée la position de la masselotte sur son axe. On obtient une courbe, une sinusoïde amortie, dans laquelle on voit la position de la masselotte – et l’élongation du ressort – varier en fonction du temps. Mais il aussi est possible de représenter ce même mouvement dans un espace plus abstrait encore, appelé espace des phases, où l’une des coordonnées représente la position de la masselotte, et l’autre sa vitesse (positive ou négative par rapport à une orientation choisie). On obtient alors une espèce d’escargot qui montre visuellement comment la vitesse et la position de la masselotte sont reliées.
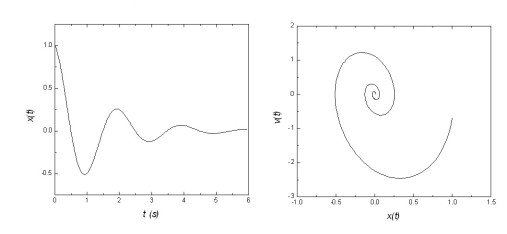
Cette représentation est très adaptée à l’étude de systèmes dits chaotiques, dans laquelle la dynamique du système est imprévisible : la représentation temporelle des processus ne montre que désordre, mais l’espace des phases associé révèle souvent des structures, appelées attracteurs étranges, autour desquelles semblent converger les trajectoires par ailleurs brouillonne du système étudié :

Ce que l’on constate avec ces exemples tirés de la mécanique, c’est que l’abstraction croissante des représentations s’accompagne en vérité d’un gain de compréhension de la structure intime du système étudié. Dans le domaine de l’économie, peut-on faire de même ? Mais oui, et c’est essentiel.
Je m’en tiendrai à un seul exemple, qui par les temps qui courent devrait être connu et compris par tous : il s’agit de ce que l’on appelle la courbe de l’éléphant, initialement due à l’économiste Branko Milanovic et récemment mise à jour par une équipe dont faisait partie Thomas Piketty, lequel en donne la nouvelle version dans son dernier livre (Capital et Idéologie, Seuil, 2019). Regardons-la sans plus tarder :

Cette courbe tire son nom de la forme qu’elle avait dans l’étude d’origine, mais Slate (à qui j’ai volé l’image ici) y voit plutôt un brontosaure ou le monstre du Loch Ness. Quoi qu’il puisse en être, cette courbe utilise comme les précédentes un espace abstrait pour mettre en valeur un phénomène qui resterait autrement caché ; elle vaut donc le coup que nous nous y arrêtions un moment.
Intéressons-nous d’abord à l’axe horizontal de la courbe. Il est étiqueté « Catégories de revenue (centiles) ». Kezaco ? Eh bien, considérons l’ensemble des êtres humains adultes à un moment donné, et classons-les par ordre croissant de revenu – les plus pauvres à gauche, les plus riches à droite (comme il se doit). Disons que nous sommes 5 milliards en âge de gagner notre vie ; nous divisons cet ensemble en cent sous-ensembles de 50 millions chacun, regroupant d’abord les 50 millions les plus pauvres, puis les suivants, en finissant par les 50 millions les plus riches. Chacun de ces ensembles forme un centile de revenu, et chaque être humain peut être associé au centile auquel il appartient.
De fait, il est intéressant de découper davantage le dernier centile, celui des 1% les plus riches en termes de revenus, et d’y distinguer dix sous-groupes de 5 millions d’habitants. Le dernier de ceux-ci est le groupe des un pour mille les plus riches, noté 99.9 dans le graphique. Nous pouvons de même découper ce dernier groupe et y distinguer les 500 000 personnes qui font partie des un sur dix-mille les plus riches, noté 99.99, et enfin identifier le groupe des un sur cent mille les plus riches, noté 99.999 dans le graphique. Dans la mesure où ce groupe comporte encore tout de même 50 000 personnes, on pourrait même identifier les quelque 5000 membres du club « un sur un million », mais cela n’apparait pas dans le graphique.
En ordonnée, on voit la croissance cumulée des revenus de chaque groupe entre 1980 et 2016. On constate par exemple qu’une personne du 40e centile – qui est donc la plus riche des 40% les plus pauvres – gagne deux fois plus en 2016 qu’en 1980 ; ses voisins plus pauvres se sont un peu plus enrichis que lui, et ceux de droite un peu moins. Dans l’ensemble, l’extrême pauvreté a reculé et c’est bien sûr une excellente nouvelle. Les classes moyennes mondiales – les 70% à 90% de revenus les plus élevés – ont en revanche bien peu profité de la croissance mondiale durant cette période ; seuls les plus riches ont vu leurs revenus s’envoler, et les plus privilégiés d’entre eux encore bien plus – c’est la trompe de l’éléphant.
De nombreuses analyses de cette courbe existent ; outre le livre passionnant déjà cité, on pourra aussi lire un article très accessible ici. On y apprend en passant que les plus pauvres en France sont plus riches que 70% des personnes dans le monde, ce qui fait froid dans le dos.
Mais le plus important, peut-être, est qu’une fois compris son fonctionnement, ce graphique lumineux se passe presque de commentaires. De même que l’espace des phases permit à Poincaré et à ses successeurs de percevoir l’ordre qui sous-tend le chaos apparent des systèmes dynamiques complexes, la vision des résultats économiques réfractés à travers le prisme des niveaux de revenus différents permet de constater immédiatement qui en profite – et de percevoir le chaos qui nous guette sous l’apparence du nouvel ordre économique mondial.
Yannick Cras
Le nombre imaginaire









0 commentaires