Le silence régna un court instant sur le bureau de Galois, nous donnant à tous le temps d’assimiler ce que nous venions de conclure. J’en avais pour ma part bien besoin. Mon treillis de concepts subjectifs – tout ce que je suis capable de percevoir et de penser – ne peut contenir aucune symétrie, car je n’aurais alors aucun moyen de distinguer deux concepts symétriques, qui pour moi n’en feraient qu’un. Pour autant, cela n’implique pas, d’après Galois, que mon cerveau ait besoin en pratique d’effectuer le travail extrêmement coûteux d’éliminer ces symétries dans la structure – quelle qu’elle soit – qui encode physiquement ce treillis. C’est un peu comme si ma conscience émergeait magiquement de son substrat physique, gommant d’un geste les éventuelles symétries, les confondant en un seul concept. Sans opérer le moindre calcul. On serait troublé à moins.

Corty reprit ses esprits le premier, avant même un Galois pensif qui gribouillait on ne sait quoi sur sa feuille en réfléchissant :

­– Maître, si je puis me permettre, pourrions-nous revenir sur cette histoire de fusion de concepts symétriques? Yannick et moi avons joué avec l’idée en regroupant des concepts symétriques au même endroit, et en constatant que, ce faisant, nous faisions aussi se recouvrir les flèches qui en partaient. Est-il possible de formaliser cette opération?

Galois cligna des yeux, lut rapidement ce que venait d’écrire Corty, et se redressa sur sa chaise.

– Excellente idée. J’aurais dû vous le proposer. Pour formaliser cette histoire de fusion, j’imaginerais bien passer par ce que l’on appelle une relation d’équivalence.

– Mais oui, bien sûr! M’exclamai-je. C’est évident maintenant!

– Pas pour moi, intervint le caillou.

– Voulez-vous alors, proposa Galois, nous expliquer comment cela fonctionne?

– En math, repris-je excité, une relation d’équivalence sur un ensemble est une relation qui relie certains éléments de cet ensemble; on peut par exemple écrire a≋b pour dire que deux éléments a et b sont reliés.

– Pour la relation de généralisation, releva Corty, nous avons employé le symbole a≼b. Pourquoi en choisir un autre?

– Parce qu’une relation d’équivalence n’a pas tout à fait les mêmes propriétés qu’une relation d’ordre partiel. Cette dernière, nous l’avons vu, est réflexive (tout élément est lié à lui-même, a≼a), antisymétrique (si a≼b et b≼a, alors a=b), et transitive (si a≼b et b≼c, alors a≼c). Une relation d’équivalence est également réflexive et transitive, mais elle est aussi symétrique : a≋b est vrai si et seulement si b≋a, a et b pouvant être différents. Or, il est facile de voir que la relation qui relie deux concepts symétriques – c’est-à-dire tels que l’un soit l’image de l’autre par un automorphisme – est une relation d’équivalence. Tout concept est relié à lui-même par l’automorphisme identité; si un concept a se transforme en un concept b par un automorphisme, alors a est l’image de b par l’automorphisme inverse; et comme la composition de deux automorphismes est un automorphisme, si a donne b par un automorphisme f et si b donne c par un automorphisme g, alors a donne c par l’automorphisme qui applique f suivi de g.

– Très bien, salua Galois. Je propose donc de conserver votre notation ≋ et d’appeler cette relation entre concepts équivalence conceptuelle.

– Ensuite, on regroupe simplement chaque concept avec tous ceux qui lui sont conceptuellement équivalents. On obtient ainsi des sous-ensembles non vides et disjoints de concept, que l’on appelle des classes d’équivalence. Chaque concept appartient à exactement une classe. Dans chaque classe, tous les concepts sont équivalents. En revanche, deux concepts choisis dans deux classes différentes ne le sont jamais. Et voilà, nos « concepts fusionnés », ce sont ces classes d’équivalence! Ce ne sont rien d’autre que des paquets de concepts regroupés au même endroit, comme Corty l’a fait sur ses dessins.

– Intéressant, dit Galois. Vous noterez au passage que nous obtenons maintenant un nouveau type de concepts par un mécanisme qui n’a rien à voir avec la construction d’un treillis de Galois; c’est bien pourquoi il est souhaitable de généraliser nos raisonnements le plus possible.

– Je vois, intervint Corty, mais quid des flèches? Nous avons vu qu’elles se fusionnaient aussi.

– En effet, repris-je. Nous pouvons modéliser cela en introduisant tout d’abord une nouvelle relation de généralisation sur nos classes d’équivalence elles-mêmes. Si A et B sont deux classes d’équivalence, je noterai A≼B s’il existe au moins un concept a dans la classe A et un concept b dans la classe B, tels que a spécialise b. Cette relation est une relation d’ordre partiel, et nous pouvons donc dessiner des flèches entre classes. Ces nouvelles flèches « fusionnent » en quelque sorte les flèches qui relient nos concepts d’origine.

– Il faudrait, bien sûr, prouver tout cela formellement, intervint Galois. Par exemple, nous savons que cette nouvelle relation est réflexive, car toute classe C contient au moins un concept qui bien sûr se spécialise lui-même, donc par définition C≼C.

– Facile ! s’écria le caillou.

– La suite l’est beaucoup moins. Nous devons, par exemple, vérifier que la relation est antisymétrique. Si A≼B et B≼A, alors il existe a1 dans la classe A et b1 dans B tels que a1≼b1. Par ailleurs il existe aussi a2 dans A et b2 dans B tels que b2≼a2. Mais en quoi cela implique-t-il que A et B soient identiques?

– Je sèche, dit joyeusement le caillou. Je suis un littéraire, moi.

– Je crois que je vois, hésitai-je. Comme a2 et a1 sont dans la même classe d’équivalence, il existe un automorphisme f qui transforme l’un en l’autre: a2 = f(a1). On sait aussi qu’un automorphisme préserve l’ordre ; comme a1 ≼ b1, on déduit que a2 = f(a1) ≼f(b1). Enfin, f(b1), que je noterai b3, appartient également à la classe B, car il est conceptuellement équivalent à b1 par définition.

– Continuez, dit Galois en hochant la tête.

– Nous avons donc, dans la classe B, deux concepts équivalents b2 et b3 tels que b2≼a2 et a2≼b3. Donc b2≼b3. Mais ça… ce n’est possible que si b2 et b3 sont identiques.

– En effet, dit Galois. C’est dû à une propriété pas si évidente que ça: dans un treillis fini, l’image d’un élément par un automorphisme n’est comparable avec lui que si les deux sont égaux. Sinon, on pourrait construire des chaînes ascendantes infinies du type a≼ f(a) ≼ f(f(a))… où tous les éléments sont différents; or ce n’est pas possible puisque le treillis est fini. C’est une preuve informelle, mais restons-en là, car nous allons manquer de temps.

En effet : Corty dessinait sur le tableau un bonhomme en train de bailler. Je m’empressai de conclure.

– Donc : comme b2≼a2 et a2≼b3=b2, on déduit que b2=a2=b3; les deux classes A et B sont identiques, et ma relation est bien antisymétrique. Ouf!

– Vous voyez? dit Galois au caillou. Raisonner sur les treillis peut être fort complexe. Nous ferons donc l’impasse sur la preuve que la relation d’ordre entre classes est aussi transitive.

– Je vous crois sur parole, répondit l’œil de taureau d’une voix mal assurée.

– De même, nous devrions nous assurer que l’ensemble des classes d’équivalence, structuré par l’ordre proposé par Yannick, est bien un treillis. Ce n’est en rien évident, car je constate que la relation ≋ n’est pas ce que l’on appelle une congruence, ce qui nous aurait garanti le résultat. Hmmm, il va falloir que j’y réfléchisse.

– Rien compris, signala le caillou.

– Quoi qu’il en soit, intervins-je, nous avons au moins établi la signification d’une flèche entre deux classes d’équivalence. Il y a une entre deux classes A et B si A≼B et s’il n’y a aucune autre classe C telle que A≼B≼C. Or, nous avons de la chance : si vous avez une flèche entre un concept a et un concept b, et si a est équivalent à un autre concept c via un automorphisme f, alors nécessairement il y a également une flèche entre c et fb), lequel appartient à la même classe que b. Donc, quand vous fusionnez a et c, vous pourrez aussi fusionner b et f(b), et donc les deux flèches entre a et b d’une part, et entre c et f(b) d’autre part. Dans les deux cas vous obtiendrez la flèche qui part de la classe de a (et de c) vers la classe de b (et de fd(b). Cela explique pourquoi Corty et moi avons pu facilement fusionner les flèches de nos dessins. Un peu comme ceci (je dessinai maladroitement sur le tableau, mais Corty eut la gentillesse de corriger mon dessin au vol):

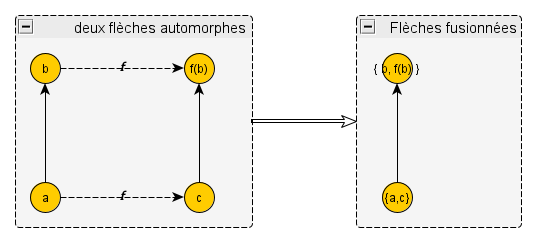
– Tout à fait, commenta Galois. Il faut juste noter que dans le cas général, a et c pourraient être identiques, ou bien b et f(b) ; et il peut y avoir plusieurs flèches partant de a ou arrivant sur b. Quand plusieurs flèches partent (ou arrivent) d’un concept (et du concept équivalent), elles peuvent ou non se retrouver fusionnées en une seule, selon que leurs extrémités sont conceptuellement équivalentes ou non. Mais dans tous les cas, en fusionnant deux concepts équivalents, vous trouverez moyen de fusionner les flèches qui en partent et y arrivent.

– Chouette! écrivit Corty. Nous avons maintenant une définition de ces concepts fusionnés, y compris avec leurs flèches. Je me suis amusé, pendant ce temps, à dessiner ce que donnent mes derniers exemples de treillis quand on fusionne les concepts équivalents, c’est-à-dire qu’on les regroupe en classes. Vous voulez voir? Voici le premier:

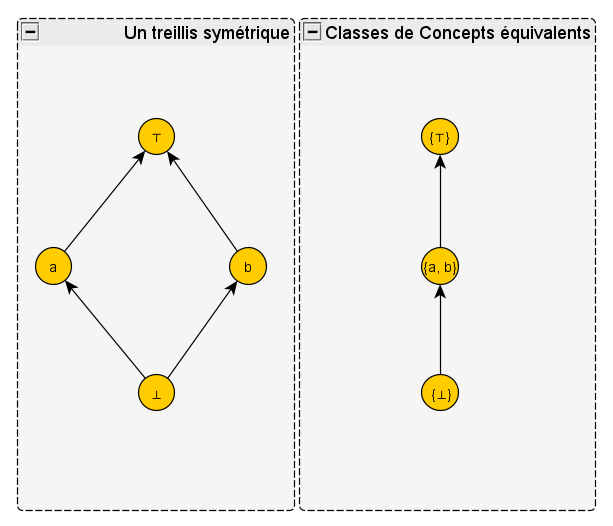
Vous le voyez, à droite j’ai dessiné les classes d’équivalence. Les deux concepts minimal et maximal sont chacun seuls dans leur classe ; les deux concepts a et b sont regroupés dans la même classe.

Mon deuxième exemple était un peu plus compliqué:

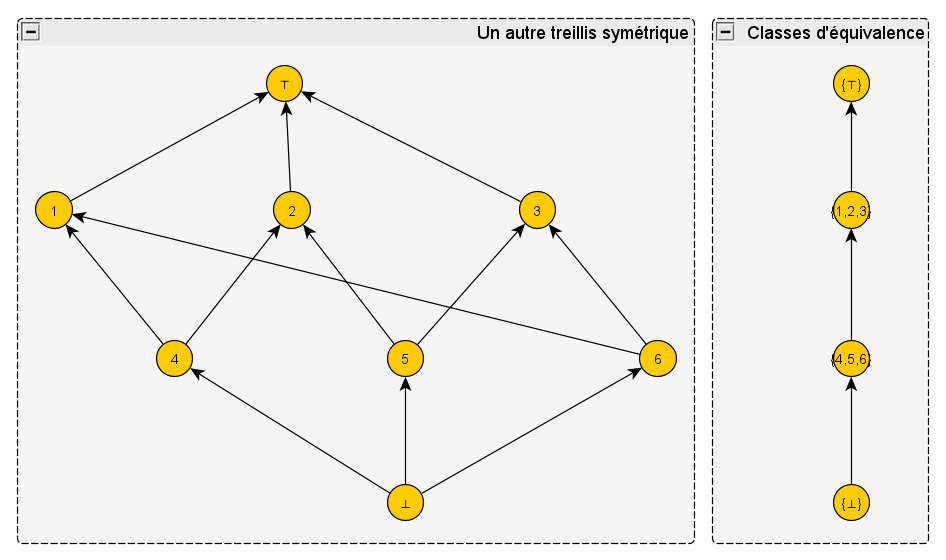
Cette fois on obtient quatre classes d’équivalence : les concepts 1,2 et 3 d’une part, les concepts 4,5 et 6 de l’autre, et les deux concepts minimal et maximal avec chacun leur classe. Vous notez aussi que les six flèches du milieu ont été fusionnées en une seule, ainsi que les trois flèches du haut et les trois du bas.

– Nom d’un petit bonhomme! s’écria Galois. Vos dessins sont brillants… et m’indiquent que nous avons un gros problème!

 

(à suivre)